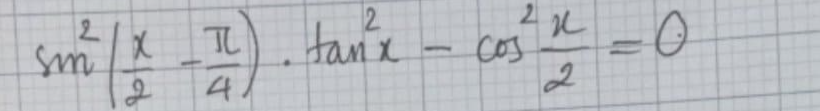Question

Answer 1

sin²\(\left(\dfrac{x}{2}-\dfrac{\pi}{4}\right).tan^2x-cos^2\dfrac{x}{2}\) = 0

⇔ \(\dfrac{1-cos\left(x-\dfrac{\pi}{2}\right)}{2}.tan^2x-\dfrac{1+cosx}{2}=0\)

⇔  \(\dfrac{1-sinx}{2}.tan^2x-\dfrac{1+cosx}{2}=0\)

⇔ tan²x - sin.tan²x - 1 - cosx = 0

⇒ sin²x - sin.cos²x - cos²x - cos³x = 0 (nhân cả 2 vế với cos²x)

⇔ cos²x - sin²x + cos³x - sinx.cos²x = 0 (đổi dấu 2 vế)

⇔ (cosx - sinx)(cosx + sinx) + cos²x (cosx - sinx)

⇔ \(\left[{}\begin{matrix}cosx-sinx=0\left(1\right)\\cosx+sinx+cos^2x=0\left(2\right)\end{matrix}\right.\)

(1) ⇔ \(cos\left(x+\dfrac{\pi}{4}\right)=0\)

(2) ⇔ cosx(cosx + 1) + sinx = 0

⇔ \(cosx.2cos^2\dfrac{x}{2}\) + 2\(sin\dfrac{x}{2}.cos\dfrac{x}{2}\) = 0

⇔ \(\left[{}\begin{matrix}cos\dfrac{x}{2}=0\\cos\dfrac{x}{2}.cosx+sin\dfrac{x}{2}=0\left(\Psi\right)\end{matrix}\right.\)

\(\left(\Psi\right)\) ⇔ \(cos\dfrac{x}{2}.\left(2cos^2\dfrac{x}{2}-1\right)+sin\dfrac{x}{2}=0\)

⇔ \(2cos^3\dfrac{x}{2}+sin\dfrac{x}{2}-cos\dfrac{x}{2}\) = 0

⇔ \(2cos^3\dfrac{x}{2}+sin\dfrac{x}{2}\left(sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}\right)-cos\dfrac{x}{2}\left(sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}\right)=0\)

⇔ \(cos^3\dfrac{x}{2}+sin^3\dfrac{x}{2}+sin\dfrac{x}{2}.cos^2\dfrac{x}{2}-sin^2\dfrac{x}{2}.cos\dfrac{x}{2}=0\)

+ Xét \(cos^3\dfrac{x}{2}=0\), nếu thỏa mãn thì kết luận nghiệm

+ Xét \(cos^3\dfrac{x}{2}\ne0\), chia cả 2 vế cho \(cos^3\dfrac{x}{2}\) đưa về phương trình bậc 3 theo \(tan\dfrac{x}{2}\)