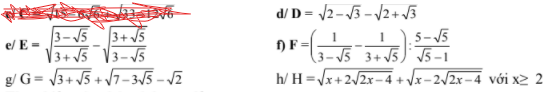Question

Answer 1

\(D=\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\Rightarrow D< 0\)( do \(\sqrt{2-\sqrt{3}}< \sqrt{2+\sqrt{3}}\))\(\Rightarrow D^2=2-\sqrt{3}+2+\sqrt{3}-2\sqrt{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}=4-2=2\Rightarrow D=-\sqrt{2}\)

(do D<0)

\(E=\sqrt{\dfrac{3-\sqrt{5}}{3+\sqrt{5}}}+\sqrt{\dfrac{3+\sqrt{5}}{3-\sqrt{5}}}=\dfrac{3-\sqrt{5}+3+\sqrt{5}}{\sqrt{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}}=\dfrac{6}{2}=3\)

 

 

Answer 2

d: Ta có: \(D=\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)

\(=\dfrac{\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}}{\sqrt{2}}\)

\(=\dfrac{\sqrt{3}-1-\sqrt{3}-1}{\sqrt{2}}=-\sqrt{2}\)

Answer 3

e. \(E=\sqrt{\dfrac{3-\sqrt{5}}{3+\sqrt{5}}}-\sqrt{\dfrac{3+\sqrt{5}}{3-\sqrt{5}}}\) 

\(=\dfrac{\sqrt{\left(3-\sqrt{5}\right)^2}-\sqrt{\left(3+\sqrt{5}\right)^2}}{\sqrt{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}}\)

\(=\dfrac{3-\sqrt{5}-3-\sqrt{5}}{\sqrt{9-5}}\) \(=\dfrac{-2\sqrt{5}}{\sqrt{4}}=-\sqrt{5}\)

f. \(F=\left(\dfrac{1}{3-\sqrt{5}}-\dfrac{1}{3+\sqrt{5}}\right):\dfrac{5-\sqrt{5}}{\sqrt{5}-1}\)

\(=\dfrac{\left(3+\sqrt{5}\right)-\left(3-\sqrt{5}\right)}{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}:\dfrac{\sqrt{5}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}\)

\(=\dfrac{2\sqrt{5}}{4}.\dfrac{1}{\sqrt{5}}=\dfrac{2}{4}=\dfrac{1}{2}\)

 

 

Answer 4

\(F=\left(\dfrac{1}{3-\sqrt{5}}-\dfrac{1}{3+\sqrt{5}}\right):\dfrac{5-\sqrt{5}}{\sqrt{5}-1}=\dfrac{3+\sqrt{5}-3+\sqrt{5}}{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}.\dfrac{\sqrt{5}-1}{5-\sqrt{5}}=\dfrac{\sqrt{5}}{2}.\dfrac{1}{\sqrt{5}}=\dfrac{1}{2}\)

Answer 5

h. \(H=\sqrt{x+2\sqrt{2x-3}}+\sqrt{x-2\sqrt{2x-4}}\)

\(=\sqrt{x+2\sqrt{2\left(x-2\right)}}+\sqrt{x-2\sqrt{2\left(x-2\right)}}\)

\(=\sqrt{\left(x-2\right)+2\sqrt{2\left(x-2\right)}+2}+\sqrt{\left(x-2\right)-2\sqrt{2\left(x-2\right)}+2}\) ( thêm bớt )

\(=\sqrt{\left(x-2+\sqrt{2}\right)^2}+\sqrt{\left(x-2-\sqrt{2}\right)^2}\)

\(=x-2+\sqrt{2}+x-2-\sqrt{2}\)  \(=2x-4\) 

Answer 6

g. \(G=\sqrt{3+\sqrt{5}}+\sqrt{7-3\sqrt{5}}-\sqrt{2}\)

\(\Rightarrow G\sqrt{2}=\sqrt{6+2\sqrt{5}}+\sqrt{14-6\sqrt{5}}-\sqrt{4}\)

\(\Rightarrow G\sqrt{2}=\sqrt{\left(1+\sqrt{5}\right)^2}+\sqrt{\left(3-\sqrt{5}\right)^2}-\sqrt{4}\)

\(\Rightarrow G\sqrt{2}=1+\sqrt{5}+3-\sqrt{5}-2\)

\(\Rightarrow G\sqrt{2}=2\)

\(\Rightarrow G=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)