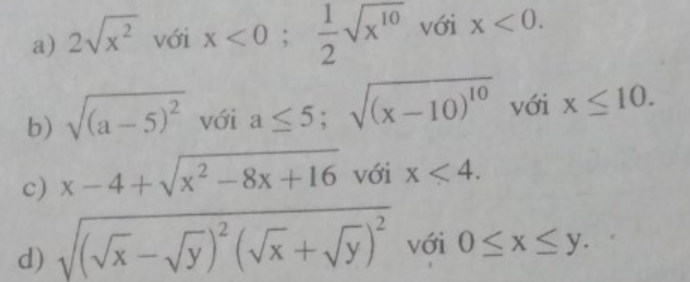a. \(2\sqrt{x^2}=2\left|x\right|=-2x\)
\(\dfrac{1}{2}\sqrt{x^{10}}=\dfrac{1}{2}\left|x^5\right|=-\dfrac{1}{2}x^5\)
b.
\(\sqrt{\left(a-5\right)^2}=\left|a-5\right|=5-a\)
\(\sqrt{\left(x-10\right)^2}=\left|\left(x-10\right)^5\right|=\left(10-x\right)^5\)
c.
\(x-4+\sqrt{x^2-8x+16}=x-4+\sqrt{\left(x-4\right)^2}=x-4+\left|x-4\right|\)
\(=x-4+4-x=0\)
d.
\(\sqrt{\left(\sqrt{x}-\sqrt{y}\right)^2\left(\sqrt{x}+\sqrt{y}\right)^2}=\left|\sqrt{x}-\sqrt{y}\right|.\left|\sqrt{x}+\sqrt{y}\right|\)
\(=-\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)=-\left(x-y\right)=y-x\)
Đúng 3
Bình luận (0)
