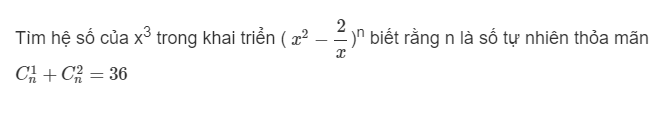Lời giải:
\((x^2+\frac{2}{x})^n=\sum \limits_{k=0}^nC^k_n(x^2)^k(\frac{2}{x})^{n-k}=\sum \limits_{k=0}^nC^k_nx^{3k-n}.2^{n-k}\)
$3k-n=3\Leftrightarrow n=3k-3$
Hệ số của $x^3$ là:\(C^{k}_{3k-3}.2^{2k-3}=101376=2^{10}.3^2.11(*)\)
$\Rightarrow 2k-3\leq 10\Rightarrow k\leq 6,5$
Vậy $1,5\leq k\leq 6,5$ nên $k=2,3,4,5,6$
Thay vô $(*)$ ta có $k=5$ suy ra $=3.5-3=12$