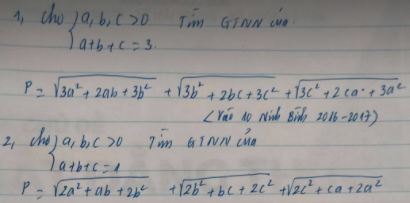\(\sqrt{3a^2+2ab+3b^2}=\sqrt{\left(a+b\right)^2+\left(2a^2+2b^2\right)}\ge\sqrt{\left(a+b\right)^2+\left(a+b\right)^2}=\sqrt{2}\left(a+b\right)\)
Tương tự: \(\sqrt{3b^2+2bc+3c^2}\ge\sqrt{2}\left(b+c\right)\) ; \(\sqrt{3c^2+2ca+3a^2}\ge\sqrt{2}\left(c+a\right)\)
Cộng vế:
\(P\ge2\sqrt{2}\left(a+b+c\right)=6\sqrt{2}\)
Dấu "=" xảy ra khi \(a=b=c=1\)
2.
\(\sqrt{2a^2+ab+2b^2}=\sqrt{\dfrac{1}{2}\left(a+b\right)^2+\dfrac{3}{2}\left(a^2+b^2\right)}\ge\sqrt{\dfrac{1}{2}\left(a+b\right)^2+\dfrac{3}{4}\left(a+b\right)^2}=\dfrac{\sqrt{5}}{2}\left(a+b\right)\)
Tương tự: \(\sqrt{2b^2+bc+2c^2}\ge\dfrac{\sqrt{5}}{2}\left(b+c\right)\) ; \(\sqrt{2c^2+ca+2a^2}\ge\dfrac{\sqrt{5}}{2}\left(c+a\right)\)
Cộng vế:
\(P\ge\sqrt{5}\left(a+b+c\right)=\sqrt{5}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)