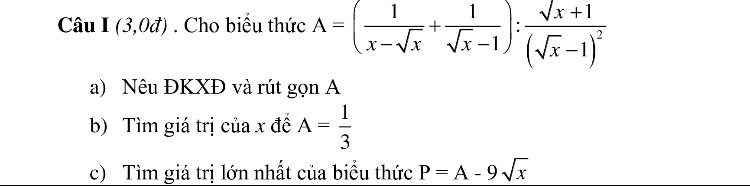a) ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)
Ta có: \(A=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\)
\(=\left(\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\right)\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
b) Để \(A=\dfrac{1}{3}\) thì \(\dfrac{\sqrt{x}-1}{\sqrt{x}}=\dfrac{1}{3}\)
\(\Leftrightarrow3\sqrt{x}-3=\sqrt{x}\)
\(\Leftrightarrow2\sqrt{x}=3\)
\(\Leftrightarrow\sqrt{x}=\dfrac{3}{2}\)
hay \(x=\dfrac{9}{4}\)(thỏa ĐK)
tử số của phân số cuối là \(\sqrt{x+1}\) hay \(\sqrt{x}+1\) thế bạn