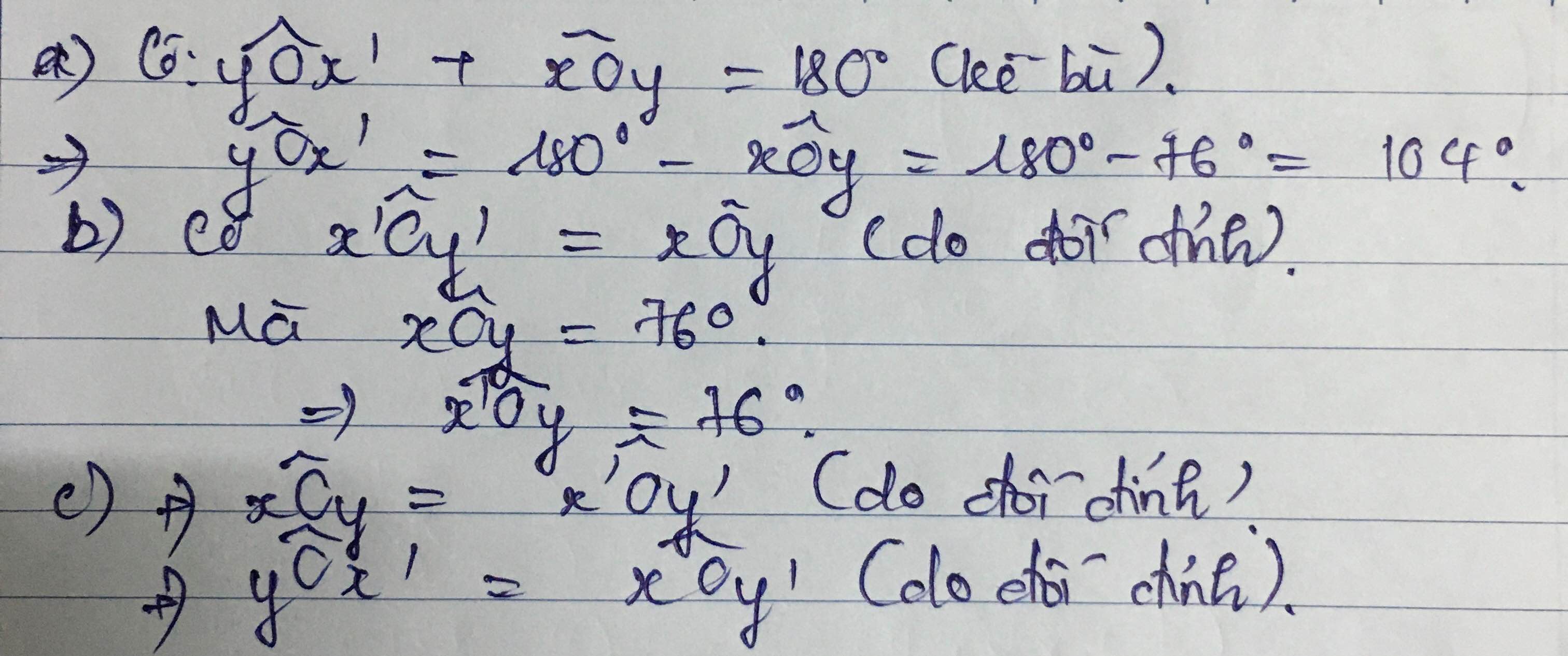Học tại trường
Chưa có thông tin
Đến từ
Chưa có thông tin , Chưa có thông tin
Số lượng câu hỏi
3
Số lượng câu trả lời
2829
Điểm GP
716
Điểm SP
2174
Người theo dõi (99)
Đang theo dõi (4)


Câu trả lời:
Chọn a. Vì từ "áo dài" chỉ một loại áo

Câu trả lời:
Bài này bị lỗi nên t gửi lại = ảnh nhé