Chứng minh rằng phương trình  sau luôn có ít nhất 3 nghiệm thực với mọi m

\(\left(m^2+1\right).x^5-2m^2.x^3-4x+m^2+1=0\)
 P/s: Câu số 5 trong đề thi cuối học kỳ 2 lớp 11 của trường THPT  Phạm Hồng Thái Hà Nội
Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý , giúp đỡ em tham khảo  với ạ!
Em cám ơn nhiều ạ!

 Bài Toán Về Số Học:
 Trên bảng có viết các số  4 ; 5; 6 ; 7; 8 ; 9. Mỗi bước,  người ta chọn  2 số  x ; y  trên bảng, xóa đi và thay bằng  hai số  \(x+y+\sqrt{x^2+y^2}\)   và \(x+y-\sqrt{x^2+y^2}\).  Chứng minh rằng , trong mọi thời điểm, các số trên bảng đều lớn hơn 1 và luôn có một số nhỏ hơn 7.
 P/s:  Bài toán được biên soạn bởi thầy Võ Quốc Bá Cẩn và thầy Trần Quốc Anh
Em nhờ quý thầy cô giáo và các bạn yêu toán gợi ý , giúp đỡ với ạ! Em cám ơn nhiều ạ!

Biết rằng   \(9x^3-6x-8=0\)  có  ít nhất 1 nghiệm thực là  \(x=a\) . Tính giá trị của biểu thức sau         \(P=\left(a+2\right).\sqrt{3a^2-4a+2}\)
P/s:   Tài liệu được biên soạn bởi thầy Võ Quốc Bá Cẩn và thầy Trần Quốc Anh ( Hà Nội)
Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ với ạ!
Em cám ơn nhiều ạ!

Tính Nhanh \(A=\left(1+12\right).\left(1+13\right).\left(1+14\right).\left(1+15\right).\left(1+16\right).\)
P/s: Em nhờ quý thầy cô giáo và các bạn yêu toán gợi ý và giúp đỡ với ạ!
Em cám ơn nhiều ạ!

Cho tam giác ABC nhọn, các đường cao  BM và CN cắt nhau tại H.
a) Chứng minh  rằng tứ giác AMHN nội tiếp đường tròn và xác định vị trí tâm I của đường tròn đó.
b) Gọi D là 1 điểm thuộc cạnh BC ( D khác B và D khác C). Đường tròn ngoại tiếp tam giác  BDN và đường tròn ngoại tiếp  tam giác CDM cắt nhau tại điểm thứ hai là E. Chứng minh rằng điểm E thuộc đường tròn ngoại tiếp tam giác AMN.
c)  Gọi K là  một điểm di động trên nửa đường tròn đường kính  BC ( Cung chứa điểm M) và  Q là chân  đường vuông góc hạ từ K xuống BC. Tìm vị trí điểm K  để tổng KQ+  BQ đạt giá trị lớn nhất .
P/s:  Đề thi thử vào lớp 10 lần 2  của trường THPT Lương Thế Vinh -- Hà Nội(  Năm 2022)

Tìm tất cả các cặp số nguyên dương \(\left(x;y\right)\) thỏa mãn điều kiện
\(x^2.y^2-2.x.y+141=4x^2+36y^2+7x+21y\)
P/s:  Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em tham khảo với ạ!
Em cám ơn nhiều lắm ạ!

Tìm tất cả các số nguyên dương n thỏa mãn \(n^3-5n+10\)  là  một lũy thừa của  2.
P/s:  Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em tham khảo với ạ ạ!

Tìm tất cả các số nguyên dương n thỏa mãn  \(3^n+n^2+23\)  là số chính phương.
P/s: Em nhờ quý thầy cô giáo và các bạn  yêu toán gợi ý , giúp đỡ em tham khảo  với ạ
Em cám ơn nhiều lắm ạ!

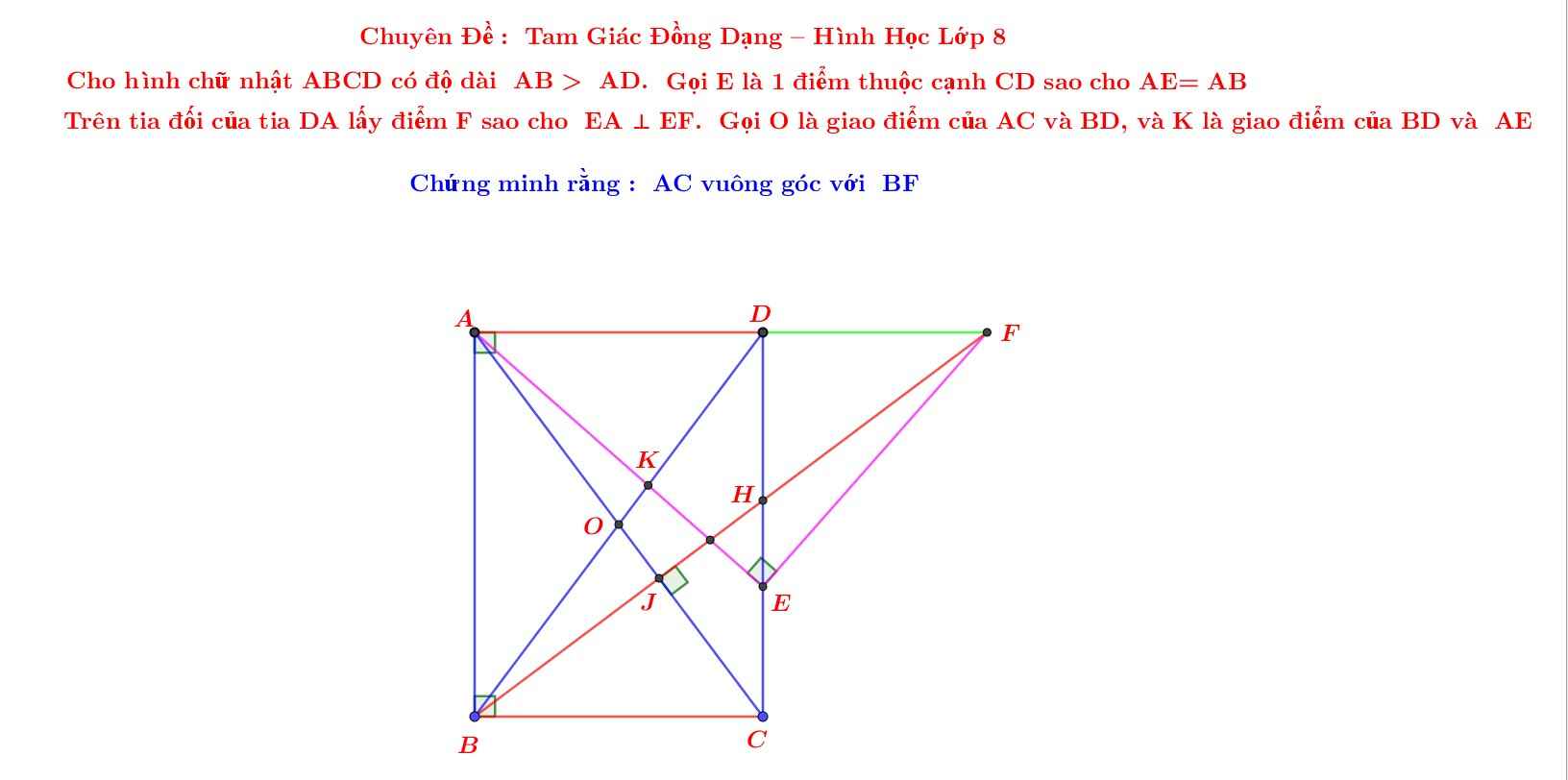
Cho hình chữ nhật ABCD có độ dài AB > AD.  Gọi O là giao điểm của  AC và BD. Gọi  E là 1 điểm thuộc cạnh CD sao cho  AE =  AB. Trên tia đối của tia DA lấy điểm F sao cho  EF vuông góc với  AE.
Chứng minh rằng AC vuông góc với  BF.
P/s:  Em nhờ quý thầy cô giáo và các bạn bè yêu toán gợi ý giúp đỡ em tham khảo với ạ
Em cám ơn nhiều lắm ạ!