Cho tam giác DEF, điểm I nằm trong tam giác và cách đều ba cạnh của nó. Chứng minh I là điểm chung của ba đường phân giác của tam giác DEF ?
Bài 6: Tính chất ba đường phân giác của tam giác
Bài 36 (SGK - tập 2 trang 72)
Thảo luận (3)
Bài 37 (SGK - tập 2 trang 72)
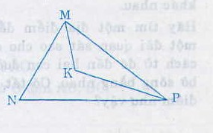
Nêu cách vẽ điểm K ở trong tam giác MNP mà các khoảng cách từ K đến ba cạnh của tam giác đó bằng nhau. Vẽ hình minh họa ?
Thảo luận (2)Hướng dẫn giảiHướng dẫn:
Vẽ điểm K ở trong tam giác MNP mà các khoảng cách từ K đến ba cạnh của tam giác đó bằng nhau tức là K là giao điểm của các đường phân giác trong tam giác MNP
Vì vậy ta chỉ cần vẽ phân giác của hai trong ba góc của ∆MNP
(Trả lời bởi Thien Tu Borum)
Bài 38 (SGK - tập 2 trang 73)
Cho hình 38.
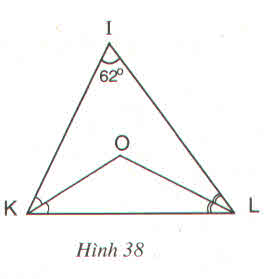
a) Tính góc KOL
b) Kẻ tia IO, hãy tính góc KIO
c) Điểm O có cách đều ba cạnh của tam giác IKL không ? Tại sao ?
Thảo luận (3)Hướng dẫn giảiHướng dẫn:
a) ∆KIL có ˆII^ = 620
nên ˆIKL+ˆILKIKL^+ILK^ = 1180
Vì KO và LO là phân giác ˆIKLIKL^, ˆILKILK^
nên ˆOKL+ˆOLKOKL^+OLK^= 1212(ˆIKL+ˆILKIKL^+ILK^)
=> ˆOKL+ˆOLKOKL^+OLK^ = 1212 1180
ˆOKL+ˆOLKOKL^+OLK^ = 590
∆KOL có ˆOKL+ˆOLKOKL^+OLK^ = 590
nên ˆKOLKOL^ = 1800 – 590 = 1210
c) Vì O là giao điểm của hai đường phân giác của ˆKK^ và ˆLL^ nên O cách đều ba cạnh của tam giác IKL
(Trả lời bởi Thien Tu Borum)
Luyện tập - Bài 39 (SGK - tập 2 trang 73)
Cho hình 39 :
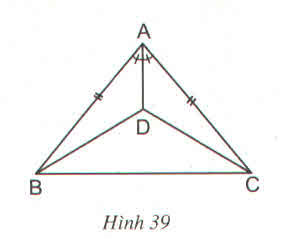
a) Chứng minh \(\Delta ABD=\Delta ACD\)
b) So sánh góc DBC và góc DCB
Thảo luận (3)Hướng dẫn giảia) Căn cứ các kí hiệu đã cho trên hình của bài 39 ta có: ∆ABD và ∆ACD có:
AB = AC
AD là cạnh chung
=> ∆ABD = ∆ACD
b) Vì ∆ABD = ∆ACD
=> BD = CD => ∆BCD cân tại D
=>
(Trả lời bởi Tuyết Nhi Melody)
Luyện tập - Bài 40 (SGK - tập 2 trang 73)
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh điểm A, G, I thẳng hàng ?
Thảo luận (3)Hướng dẫn giải
Gọi giao điểm của BG với AC là M;
CG với AB là N
Vì G là trọng tâm của ∆ ABC
nên BM, CN, là trung tuyến
Mặt khác ∆ABC cân tại A
Nên BM = CN
Ta có GB = BM; GC = CN (t/c trọng tâm của tam giác)
Mà BM = CN nên GB = GC
Do đó: ∆AGB = ∆AGC (c.c.c)
=> => G thuộc phân giác của
Mà ∆ABI = ∆ACI (c.c.c)
=> => I thuộc phân giác của
Vì G, I cùng thuộc phân giác của nên A, G, I thẳng hàng
(Trả lời bởi Tuyết Nhi Melody)
Luyện tập - Bài 41 (SGK - tập 2 trang 73)
Hỏi trọng tâm của một tam giác đều có cách đều 3 cạnh của nó hay không ? Vì sao ?
Thảo luận (3)Hướng dẫn giải
GT tam giác ABC đều
G là trọng tâm tam giác
KL G cách đề ba cạnh tam giác
Trọng tâm của tam giác đều cách đều ba cạnh của nó :
Giả sử ∆ABC đều có trọng tâm G
=> GA = 2323AN; GB = 2323BM; GC = 2323EC
Vì ∆ABC đều nên ba trung tuyến AN, BM, CE bằng nhau
=> GA = GB = GC
Do đó: ∆AMG = ∆CMG (c.c.c)
=> ˆAMG=ˆCMGAMG^=CMG^
Mà ˆAMG=ˆCMGAMG^=CMG^ = 1800
=> ˆAMGAMG^ = 900
=> GM ⊥ AC tức là GM khoảng cách từ G đến AC
Chứng minh tương tự GE, GN là khoảng cách từ G đến AB, AC
Mà GM =1313BM; GN = 1313AN; EG = 1313EC
Và AN = BM = EC nên GM = GN = GE
Hay G cách đều ba cạnh của tam giác ABC
(Trả lời bởi Tâm Trần Huy)
Luyện tập - Bài 42 (SGK - tập 2 trang 73)
Chứng minh định lí :
Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân
Gợi ý : Trong tam giác ABC, nếu AD vừa là đường trung tuyến vừa là đường phân giác thì kéo dài AD một đoạn \(DA_1\) sao cho \(DA_1=AD\)
Thảo luận (3)Hướng dẫn giảicho em giải khác nhé
D thuộc phân giác góc A suy ra DH = DG ( tính chất tia phân giác của một góc )
xét hai tam giác vuông BHD và CGD có
DH = DG ( cmt)
DB = DC ( gt)
do đó tam giác BHD = tam giác CGD ( cạnh huyền - góc nhọn )
suy ra góc B = góc C ( 2 góc tương ứng )
tam giác ABC có góc B = góc C suy ra tam giác ABC cân tại A
(Trả lời bởi Tâm Trần Huy)
Luyện tập - Bài 43 (SGK - tập 2 trang 73)
Đố :
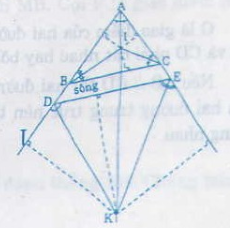
Có hai con đường cắt nhau và cùng cắt một con sông tại hai điểm khác nhau (h.40)
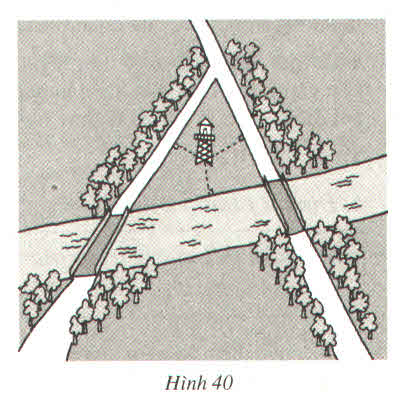
Hãy tìm một địa điểm để xây dựng một đài quan sát sao cho các khoảng cách từ đó đến hai con đường và đến bờ sông bằng nhau ?
Có tất cả mấy địa điểm như vậy ?
Thảo luận (3)Hướng dẫn giảiHướng dẫn:
Hai con đường cắt nhau và cùng cắt một con song tạo thành tam giác ABC. Địa điểm để xây dựng trạm kiểm lâm thỏa mãn đề bài phải là giao điểm I của ba đường phân giác trong của tam giác ABC và giao điểm K của tia phân giác của góc A và hai tia phân giác của các góc ngoài ở đỉnh D và đỉnh E của tam giác ADE.
Vậy các địa điểm và các khoảng cách này ngắn nhất để xây dựng trạm kiểm lâm là I, K
(Trả lời bởi Thien Tu Borum)
Bài 45 (Sách bài tập - tập 2 - trang 46)
Cho tam giác ABC cân tại A. Gọi G là trọng tâm của tam giác, gọi I là giao điểm các đường phân giác. Chứng minh rằng ba điểm A, G, I thẳng hàng.
Thảo luận (1)Hướng dẫn giải
G là trọng tâm của \(\Delta ABC\) nên G thuộc đường trung tuyến AM (1)
Trong tam giác cân, đường trung phân giác của góc ở đỉnh đồng thời là đường trung tuyến nên I cũng thuộc đường trung tuyến AM. (2)
Từ (1) và (2) suy ra A, G, I thẳng hàng.
(Trả lời bởi Hải Ngân)
Bài 46 (Sách bài tập - tập 2 - trang 46)
Cho tam giác ABC. Hãy tìm một điểm sao cho khoảng cách từ điểm đó đến mỗi đường thẳng AB, BC, CA là bằng nhau, đồng thời khoảng cách này là ngắn nhất ?
Thảo luận (1)Hướng dẫn giải
Điểm cách đều các đường thẳng AB và AC nằm trên các đường phân giác (trong và ngoài) của góc B.
Điểm cách đều các đường thẳng AB và AC nằm trên các đường phân giác (trong và ngoài) của góc A.
Điểm cách đều các đường thẳng AB, BC, CA là giao điểm của các đường phân giác trên, đó là bốn điểm I, K, M, N.
Để khoảng cách nói trên là ngắn nhất, ta chọn điểm I, giao điểm của các đường phân giác trong của \(\Delta ABC.\)
(Trả lời bởi Hải Ngân)