Cho tam giác \(ABC\) vuông tại \(A\) có \(AB=AC\). Qua \(A\) kẻ đường thẳng \(xy\) sao cho \(B,C\) nằm cùng phía với \(xy\). Kẻ \(BD\) và \(CE\) vuông góc với \(xy\), biết \(BD=3cm\), \(CE=2cm\). Tính \(DE\)?
\(DE=6cm\).\(DE=1cm\).\(DE=5cm\).\(DE=4cm\).Hướng dẫn giải: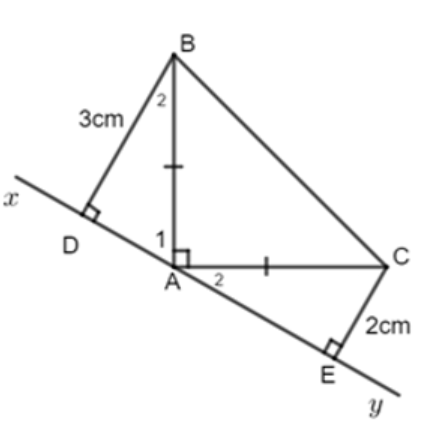
\(\Delta ABD\) vuông tại \(D\) \(\Rightarrow\widehat{A_1}+\widehat{B_2}=90^0\) (hai góc nhọn phụ nhau)
Lại có: \(\widehat{A_1}+\widehat{BAC}+\widehat{A_2}=180^0\) \(\Rightarrow\widehat{A_1}+\widehat{A_2}=180^0-\widehat{BAC}=180^0-90^0=90^0\)
\(\Rightarrow\widehat{A_2}=\widehat{B_2}\)
Khi đó ta chứng minh được \(\Delta DAB=\Delta ECA\) (cạnh huyền - góc nhọn)
\(\Rightarrow BD=AE,AD=CE\) (hai cạnh tương ứng)
Có \(DE=AD+AE=CE+BC=2cm+3cm=5cm\)

