Cho tam giác \(ABC\) có \(AB=BC=CA\), phân giác \(BD\) và \(CE\) cắt nhau tại \(O\). Chọn câu dúng
\(CE\perp AB\).\(BD\perp AC\).\(DC=BC\).\(CE\perp AB\) và \(BD\perp AC\).Hướng dẫn giải: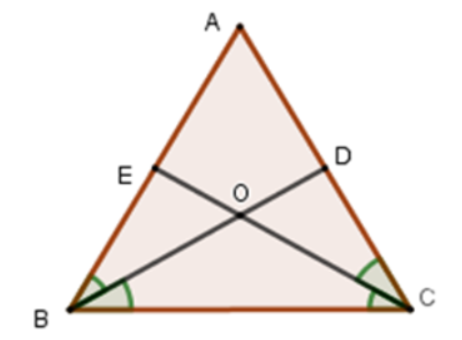
\(BD\) là phân giác \(\widehat{B}\) \(\Rightarrow\) \(\widehat{ABD}=\widehat{CBD}\)
\(CE\) là phân giác \(\widehat{C}\) \(\Rightarrow\) \(\widehat{ACE}=\widehat{BCE}\)
Khi đó ta chứng minh được \(\Delta ABD=\Delta CBD\) (c.g.c)
\(\Rightarrow\widehat{ADB}=\widehat{CDB}\) (hai góc tương ứng) mà \(\widehat{ADB}+\widehat{CDB}=180^0\) \(\Rightarrow\) \(\widehat{ADB}=\widehat{CDB}=\dfrac{180^0}{2}=90^0\) \(\Rightarrow BD\perp AC\)
Tương tự chứng minh được \(CE\perp AB\)
Do \(\Delta ABD=\Delta CBD\) nên \(AD=CD\) (hai cạnh tương ứng) (nên \(DC=BC\) là sai)

