Cho tam giác ABC có 3 góc nhọn, \(AC=b;BC=a\) , góc giữa cạnh BC và đường cao BB' là \(\widehat{CBB'}=\alpha\). Tính bán kính đường tròn ngoại tiếp tam giác ABC theo a, b và \(\alpha\).
\(R=\dfrac{\sqrt{a^2+b^2-2ab\cos\alpha}}{2\sin\alpha}\).\(R=\dfrac{\sqrt{a^2+b^2-2ab\cos\alpha}}{2\cos\alpha}\).\(R=\dfrac{\sqrt{a^2+b^2-2ab\sin\alpha}}{2\cos\alpha}\).\(R=\dfrac{\sqrt{a^2+b^2-2ab\sin\alpha}}{2\sin\alpha}\).Hướng dẫn giải: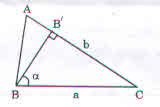
Theo định lý cosin ta có \(AB^2=a^2+b^2-2ab.\cos C\)
\(=a^2+b^2-2ab.\cos\left(90^0-\alpha\right)\)
\(=a^2+b^2-2ab.\sin\alpha\)
Theo định lý sin :
\(R=\dfrac{AB}{2\sin C}=\dfrac{\sqrt{a^2+b^2-2ab\sin\alpha}}{2\sin\left(90^0-\alpha\right)}=\dfrac{\sqrt{a^2+b^2-2ab\sin\alpha}}{2\cos\alpha}\)

