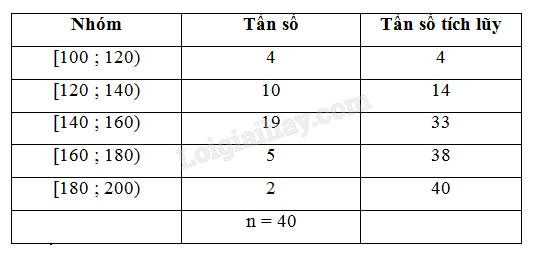
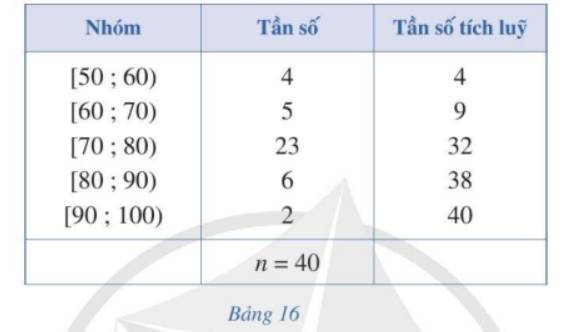
Người ta tiến hành phỏng vấn 40 người về một mẫu áo sơ mi mới. Người điều tra yêu cầu cho điểm mẫu áo đó theo thang điểm là 100. Kết quả được trình bày trong Bảng 16.
a) Trung vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị:
A. 74
B. 75
C. 76
D. 77
b, Tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng đơn vị) là:
A. \({Q_1} \approx 71;{Q_2} \approx 76;{Q_3} \approx 78\)
B. \({Q_1} \approx 71;{Q_2} \approx 75;{Q_3} \approx 78\)
C. \({Q_1} \approx 70;{Q_2} \approx 76;{Q_3} \approx 79\)
D. \({Q_1} \approx 70;{Q_2} \approx 75;{Q_3} \approx 79\)
c, Mốt của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng đơn vị) là:
A. 73
B. 74
C. 75
D. 76