Cho hàm số \(y = {x^3} - 3{x^2} + 4x - 1\) có đồ thị là \((C)\). Hệ số góc nhỏ nhất của tiếp tuyến tại một điểm \(M\) trên đồ thị \((C)\) là
A. 1 .
B. 2.
C. -1 .
D. 3 .
Cho hàm số \(y = {x^3} - 3{x^2} + 4x - 1\) có đồ thị là \((C)\). Hệ số góc nhỏ nhất của tiếp tuyến tại một điểm \(M\) trên đồ thị \((C)\) là
A. 1 .
B. 2.
C. -1 .
D. 3 .
Tính đạo hàm của các hàm số sau:
a) \(y = {\left( {\frac{{2x - 1}}{{x + 2}}} \right)^5}\)
b) \(y = \frac{{2x}}{{{x^2} + 1}}\);
c) \(y = {e^x}{\sin ^2}x\);
d) \(y = \log (x + \sqrt x )\).
Thảo luận (1)Hướng dẫn giảitham khảo:
a)\(y'\left(x\right)=5\left(\dfrac{2x-1}{x+2}\right)^4.\dfrac{\left(x+2\right)\left(2\right)-\left(2x-1\right).1}{\left(x+2\right)^2}\)
\(=\dfrac{10\left(2x-1\right)\left(x+2\right)^3}{\left(x+2\right)^4}=\dfrac{20x-50}{\left(x+2\right)^4}\)
b)\(y'\left(x\right)=\dfrac{2\left(x^2+1\right)-2x\left(2x\right)}{\left(x^2+1\right)^2}\)\(=\dfrac{2\left(1-x^2\right)}{\left(x^2+1\right)^2}\)
c)\(y'\left(x\right)=e^x.2sinxcosx+e^xsin^2x.2cosx\)
\(=2e^xsinx\left(cosx+sinxcosx\right)\)
\(=2e^xsinxcos^2x\)
d)\(y'\left(x\right)=\dfrac{1}{x\sqrt{x}}.\left(+\dfrac{1}{2\sqrt{x}}\right)\)
\(=\dfrac{1}{\sqrt{x}\left(2\sqrt{x}+\sqrt{x}+2\right)}\)
\(=\dfrac{1}{\sqrt{x}\left(3\sqrt{x}+2\right)}\)
(Trả lời bởi Bùi Nguyên Khải)
Xét hàm số luỹ thừa \(y = {x^\alpha }\) với \(\alpha \) là số thực.
a) Tìm tập xác định của hàm số đã cho.
b) Bằng cách viết \(y = {x^\alpha } = {e^{\alpha \ln x}}\), tính đạo hàm của hàm số đã cho.
Thảo luận (1)Hướng dẫn giảia: Nếu a là số nguyên dương thì TXĐ là D=R
Nếu a là số không phải nguyên dương thì TXĐ là D=R\{0}
Nếu a không là số nguyên thì TXĐ: D=R
b: \(y'=\left(x^a\right)'=\left(e^{a\cdot lnx}\right)'\)
\(=\dfrac{a}{x}\cdot e^{a\cdot lnx}=\dfrac{a}{x}\cdot x^a=a\cdot x^{a-1}\)
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Cho hàm số \(f(x) = \sqrt {3x + 1} \). Đặt \(g(x) = f(1) + 4\left( {{x^2} - 1} \right)f'(1)\). Tính \(g(2)\).
Thảo luận (1)Hướng dẫn giảiTa có: \(f'\left(x\right)=\dfrac{3}{2\sqrt{3x+1}}\)
Do đó, \(f\left(1\right)=2,f'\left(1\right)=\dfrac{3}{4}\)
Vậy \(g\left(2\right)=f\left(1\right)+4\left(2^2-1\right)f'\left(1\right)=2+12\cdot\dfrac{3}{4}=11\)
(Trả lời bởi Hà Quang Minh)
Cho hàm số \(f(x) = \frac{{x + 1}}{{x - 1}}\). Tính \(f''(1)\).
Thảo luận (1)Hướng dẫn giải\(f'\left(x\right)=\dfrac{\left(x+1\right)'\left(x-1\right)-\left(x+1\right)\left(x-1\right)'}{\left(x-1\right)^2}\)
\(=\dfrac{x-1-x-1}{\left(x-1\right)^2}=\dfrac{-2}{\left(x-1\right)^2}\)
=>\(f''\left(x\right)=\dfrac{-2\cdot\left(-2\right)\left(x-1\right)}{\left(x-1\right)^4}=\dfrac{4}{\left(x-1\right)^3}\)
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Cho hàm số \(f(x)\) thoả mãn \(f(1) = 2\) và \(f'(x) = {x^2}f(x)\) với mọi \(x\). Tính \(f''(1)\).
Thảo luận (1)Hướng dẫn giải
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = {x^3} + 3{x^2} - 1\) tại điểm có hoành độ bằng 1.
Thảo luận (1)Hướng dẫn giảiTa có: \(y'=3x^2+6x\Rightarrow\left\{{}\begin{matrix}y'\left(1\right)=9\\y\left(1\right)=3\end{matrix}\right.\)
Phương trình tiếp tuyến là: \(y=9\left(x-1\right)+3=9x-6\)
(Trả lời bởi Hà Quang Minh)
Hình 9.10 biểu diễn đồ thị của ba hàm số. Hàm số thứ nhất là hàm vị trí của một chiếc ô tô, hàm số thứ hai biểu thị vận tốc và hàm số thứ ba biểu thị gia tốc của ô tô đó. Hãy xác định đồ thị của mỗi hàm số này và giải thích.
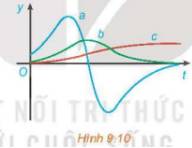
Thảo luận (1)Hướng dẫn giảiHàm số c luôn đồng biến, tức là đạo hàm của nó phải luôn không âm, do đó hàm số b là đạo hàm của hàm số c; hàm số b đồng biến trên khoảng mà hàm số a dương và nghịch biến trên khoảng mà hàm số a âm, do đó hàm số a là đạo hàm của hàm số b.
Vậy hàm số a là hàm gia tốc, hàm số b là hàm vận tốc và hàm số c là hàm vị trí của ô tô.
(Trả lời bởi Hà Quang Minh)
Vị trí của một vật chuyển động thẳng được cho bởi phương trình: \(s = f(t) = {t^3} - 6{t^2} + 9t\), trong đó t tính bằng giây và s tính bằng mét.
a) Tính vận tốc của vật tại các thời điểm t = 2 giây và t = 4 giây.
b) Tại những thời điểm nào vật đứng yên?
c) Tìm gia tốc của vật tại thời điểm t = 4 giây.
d) Tính tổng quãng đường vật đi được trong 5 giây đầu tiên.
e) Trong 5 giây đầu tiên, khi nào vật tăng tốc, khi nào vật giảm tốc?
Thảo luận (2)Hướng dẫn giải\(a,v\left(t\right)=s'\left(t\right)=3t^2-12t-9\)
Vận tốc của vật tại thời điểm t = 2s là: \(v\left(2\right)=3\cdot2^2-12\cdot2+9=-3\left(m/s\right)\)
Vận tốc của vật tại thời điểm t = 4s là: \(v\left(4\right)=3\cdot4^2-12\cdot4+9=9\left(m/s\right)\)
b, Khi vật đứng yên, ta có:
\(v\left(t\right)=0\Leftrightarrow3t^2-12t+9=0\Leftrightarrow\left[{}\begin{matrix}t=3\\t=1\end{matrix}\right.\)
c, Ta có \(a\left(t\right)=s"\left(t\right)=6t-12\)
Gia tốc của vật tại thời điểm t = 4s là \(a\left(4\right)=6\cdot4-12=12\left(m/s^2\right)\)
(Trả lời bởi Hà Quang Minh)