Bài 5: Ôn tập chương Số phức

1. Định nghĩa số phức

Mỗi biểu thức dạng \(a+bi\) trong đó  \(a,b\in R,i^2=-1\) được gọi là một số phức.

Đối với số phức \(z=a+bi\), ta nói \(a\) là phần thực  \(b\) là phần ảo của  \(z\).

Tập hợp các số phức kí hiệu là  \(C\).

2. Số phức bằng nhau 

Hai số phức bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau.

 \(a+bi=c+di\Leftrightarrow a=c;b=d\)

Chú ý:

- Mỗi số thực \(a\) được coi là một số phức với phần ảo bằng \(0\) và \(a=a+0i\). Như vậy, mỗi số thực cũng là một số phức. Ta có \(R\subset C\).

- Số phức \(0+bi\) được gọi là số thuần ảo và viết đơn giản là \(bi\).

\(bi=0+bi\)

Đặc biệt \(i=0+1i\). Số \(i\) được gọi là đơn vị ảo.

3. Biểu diễn hình học số phức

Điểm \(M\left(a;b\right)\) trong một hệ toạ độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức \(z=a+bi\).

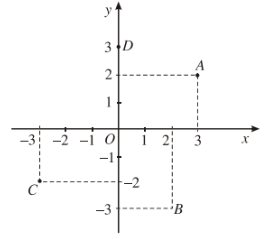
Ví dụ: Điểm \(A\left(3;2\right)\) biểu diễn số phức \(3+2i\) ;

           Điểm \(B\left(2;-3\right)\) biểu diễn số phức \(2-3i\) ;

           Điểm \(C\left(-3;-2\right)\) biểu diễn số phức \(-3-2i\) ;

           Điểm \(D\left(0;3\right)\) biểu diễn số phức \(3i\).

4. Môđun của số phức

Giả sử số phức \(z=a+bi\) được biểu diễn bởi điểm \(M\left(a;b\right)\) trên mặt phẳng tọa độ.

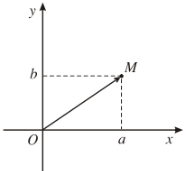
Độ dài của vectơ \(\overrightarrow{OM}\) được  gọi là môđun của số phức \(z\) và kí hiệu là \(\left|z\right|\).

Vậy \(\left|z\right|=\left|\overrightarrow{OM}\right|\) hay \(\left|a+bi\right|=\left|\overrightarrow{OM}\right|\).

Dễ thấy \(\left|a+bi\right|=\sqrt{a^2+b^2}\)

5. Số phức liên hợp 

Cho số phức \(z=a+bi\) , ta gọi \(a-bi\) là số phức liên hợp của \(z\) và kí hiệu là \(\overline{z}=a-bi\).

6. Phép cộng, trừ và nhân số phức

- Phép cộng hai số phức:

Phép cộng hai số phức được thực hiện theo quy tắc cộng đa thức.

                        \(\left(a+bi\right)+\left(c+di\right)=\left(a+c\right)+\left(b+d\right)i\)

Phép cộng số thức có các tính chất tương tự như phép cộng đa thức.

Với các số phức \(z,z',z''\) ta có:

   +) Tính chất kết hợp: \(\left(z+z'\right)+z''=z+\left(z'+z''\right)\)

   +) Tính chất giao hoán: \(z+z'=z'+z\)

- Phép trừ hai số phức:

Phép trừ hai số phức được thực hiện theo quy tắc trừ đa thức.

                        \(\left(a+bi\right)-\left(c+di\right)=\left(a-c\right)+\left(b-d\right)i\)

- Phép nhân hai số phức:

Phép nhân hai số phức được thực hiện theo quy tắc nhân đa thức rồi thay \(i^2=-1\) trong kết quả nhận được.

Tổng quát: 

                       \(\left(a+bi\right)\left(c+di\right)=\left(ac-bd\right)+\left(ad+bc\right)i\).

7. Phép chia số phức

a) Tổng và tích của hai số phức liên hợp

Cho số phức \(z=a+bi\). Ta có:

            \(z+\overline{z}=\left(a+bi\right)+\left(a-bi\right)=2a\)

            \(z.\overline{z}=\left(a+bi\right)\left(a-bi\right)=a^2-\left(bi\right)^2=a^2+b^2=\left|z\right|^2\)

Tổng của một số phức với số phức liên hợp của nó bằng hai lần phần thực của số phức đó.

Tích của một số phức với số phức liên hợp của nó bằng bình phương mô đun của số phức đó.

b) Phép chia hai số phức

Chia số phức \(c+di\) cho số phức \(a+bi\) khác \(0\) là tìm số phức \(z\) sao cho \(c+di=\left(a+bi\right)z\)

Số phức \(z\) được gọi là thương trong phép chia \(c+di\) cho \(a+bi\) và kí hiệu là

                                           \(z=\dfrac{c+di}{a+bi}\)

Tổng quát:

                                      \(\dfrac{c+di}{a+bi}=\dfrac{ac+bd}{a^2+b^2}+\dfrac{ad-bc}{a^2+b^2}i\).

Chú ý: Trong thực hành, để tính thương \(\dfrac{c+di}{a+bi}\) ta nhân cả tử và mẫu với số phức liên hợp của \(a+bi\).

8. Phương trình bậc hai với hệ số thực

Cho phương trình bậc hai \(ax^2+bx+c=0\) với \(a,b,c\in R;a\ne0\).

Xét biệt số \(\Delta=b^2-4ac\) của phương trình, ta thấy:

Khi \(\Delta=0\), phương trình có một nghiệm thực \(x=-\dfrac{b}{2a}\).

Khi \(\Delta>0\), phương trình có hai nghiệm thực phân biệt là 

                                              \(x_{1,2}=\dfrac{-b\pm\sqrt{\Delta}}{2a}\).

Khi \(\Delta< 0\), phương trình không có nghiệm thực vì không tồn tại căn bậc hai thực của \(\Delta\). Tuy nhiên xét trong tập số phức, ta vẫn có hai căn bậc hai thuần ảo của \(\Delta\) là \(\pm i\sqrt{\Delta}\). Khi đó phương trình có hai nghiệm phức là 

                                              \(x_{1,2}=\dfrac{-b\pm i\sqrt{\left|\Delta\right|}}{2a}\).

Nhận xét: 

Trên tập số phức, mọi phương trình bậc hai đều có hai nghiệm (không nhất thiết phân biệt).

Tổng quát, người ta đã chứng minh được rằng mọi phương trình bậc \(n\) \(\left(n\ge1\right)\)

               \(a_0x^n+a_1x^{n-1}+...+a_{n-1}x+a_n=0\),

trong đó \(a_0,a_1,...,a_n\in C,a_0\ne0\) đều có \(n\) nghiệm phức (các nghiệm không nhất thiết phân biệt).