Bài 1: Số phức
Nội dung lý thuyết
1. Số \(i\)
Ta đã biết các phương trình bậc hai với biệt số âm không có nghiệm thực. Phương trình bậc hai đơn giản nhất không có nghiệm thực là phương trình
\(x^2+1=0\)
Với mong muốn mở rộng tập hợp số thực để mọi phương trình bậc \(n\) đều có nghiệm, người ta đưa ra một số mới, kí hiện là \(i\) và coi nó là nghiệm của phương trình trên. Như vậy
\(i^2=-1\)
2. Định nghĩa số phức
Mỗi biểu thức dạng \(a+bi\) trong đó \(a,b\in R,i^2=-1\) được gọi là một số phức.
Đối với số phức \(z=a+bi\), ta nói \(a\) là phần thực \(b\) là phần ảo của \(z\).
Tập hợp các số phức kí hiệu là \(C\).
Ví dụ: Các số sau là những số phức: \(2+5i;-\sqrt{2}+3i;1+\left(-3\right)i\) (còn viết là \(1-3i;\)); ... Phần thực của các số trên lần lượt là \(2;-\sqrt{2};1\) và phần ảo của chúng lần lượt là \(5;3;-3\).
@37340@
3. Số phức bằng nhau
Hai số phức bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau.
\(a+bi=c+di\Leftrightarrow a=c;b=d\)
Ví dụ: Tìm các số thực \(x\) và \(y\), biết:
\(\left(2x+1\right)+\left(3y-2\right)i=\left(x+2\right)+\left(y+4\right)i\).
Giải:
Từ định nghĩa của hai số phức bằng nhau, ta có :
\(2x+1=x+2\) và \(3y-2=y+4\)
Vậy \(x=1;y=3\)
Chú ý:
- Mỗi số thực \(a\) được coi là một số phức với phần ảo bằng \(0\) và \(a=a+0i\). Như vậy, mỗi số thực cũng là một số phức. Ta có \(R\subset C\).
- Số phức \(0+bi\) được gọi là số thuần ảo và viết đơn giản là \(bi\).
\(bi=0+bi\)
Đặc biệt \(i=0+1i\). Số \(i\) được gọi là đơn vị ảo.
Ví dụ: Số \(\dfrac{1}{2}\) cũng là một số phức có phần thực là \(\dfrac{1}{2}\) và phần ảo là \(0\) ;
Số \(5i\) hay chính là \(0+5i\) là một số thuần ảo.
@55243@
4. Biểu diễn hình học số phức
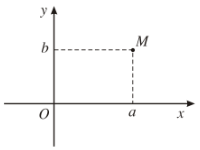
Điểm \(M\left(a;b\right)\) trong một hệ toạ độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức \(z=a+bi\).
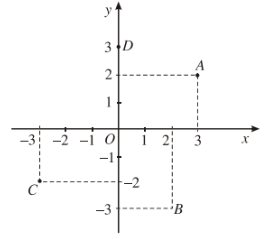
Ví dụ: Điểm \(A\left(3;2\right)\) biểu diễn số phức \(3+2i\) ;
Điểm \(B\left(2;-3\right)\) biểu diễn số phức \(2-3i\) ;
Điểm \(C\left(-3;-2\right)\) biểu diễn số phức \(-3-2i\) ;
Điểm \(D\left(0;3\right)\) biểu diễn số phức \(3i\).
5. Môđun của số phức
Giả sử số phức \(z=a+bi\) được biểu diễn bởi điểm \(M\left(a;b\right)\) trên mặt phẳng tọa độ.
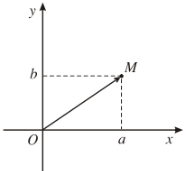
Độ dài của vectơ \(\overrightarrow{OM}\) được gọi là môđun của số phức \(z\) và kí hiệu là \(\left|z\right|\).
Vậy \(\left|z\right|=\left|\overrightarrow{OM}\right|\) hay \(\left|a+bi\right|=\left|\overrightarrow{OM}\right|\).
Dễ thấy \(\left|a+bi\right|=\sqrt{a^2+b^2}\)
Ví dụ : \(\left|3-2i\right|=\sqrt{3^2+\left(-2\right)^2}=\sqrt{13}\)
\(\left|1+i\sqrt{3}\right|=\sqrt{1+\left(\sqrt{3}\right)^2}=2\)
@31614@
6. Số phức liên hợp
Cho số phức \(z=a+bi\) , ta gọi \(a-bi\) là số phức liên hợp của \(z\) và kí hiệu là \(\overline{z}=a-bi\).
Ví dụ: +) \(z=3+\dfrac{1}{2}i\) , \(\overline{z}=3-\dfrac{1}{2}i\) ;
+) \(z=4-\sqrt{3}i\), \(\overline{z}=4+\sqrt{3}i\) ; ...
Trên mặt phẳng toạ độ, các điểm biểu diễn \(z\) và \(\overline{z}\) đối xứng nhau qua \(Ox\).

Nhận xét: \(\overline{\overline{z}}=z\) ;
\(\left|\overline{z}\right|=\left|z\right|\).
Ví dụ: \(\left|3+4i\right|=\left|3-4i\right|=5\).
@36578@