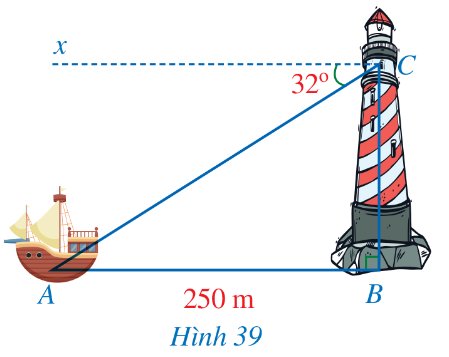
Trên mặt biển, khi khoảng cách AB từ ca nô đến chân tháp hải đăng là 250 m, một người đứng trên tháp hải đăng đó, đặt mắt tại vị trí C và nhìn về phía ca nô theo phương CA tạo với phương nằm ngang Cx một góc là \(\widehat{ACx}\) = 32° (Hình 39). Tính chiều cao của tháp hải đăng (làm tròn kết quả đến hàng phần mười của mét), biết AB // Cx và độ cao từ tầm mắt của người đó đến đỉnh tháp hải đăng là 3,2 m.