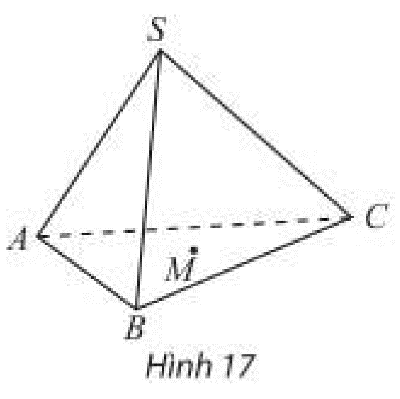
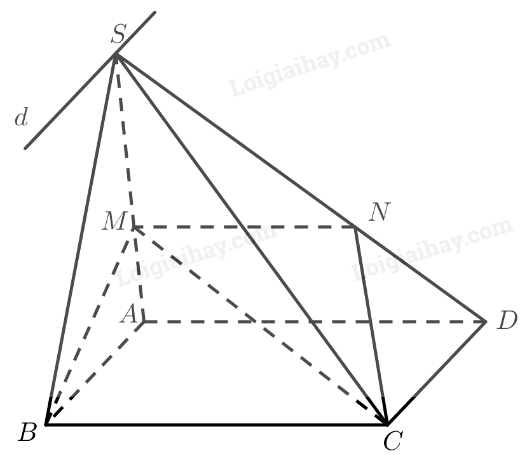
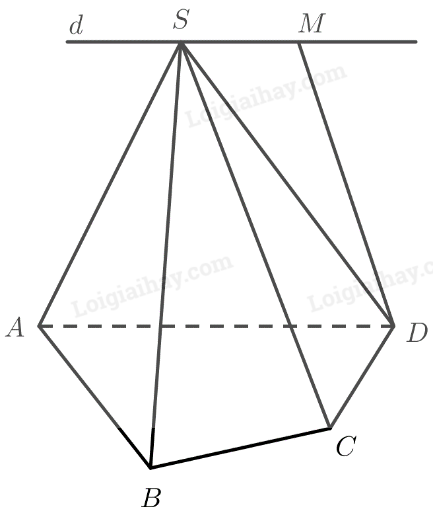
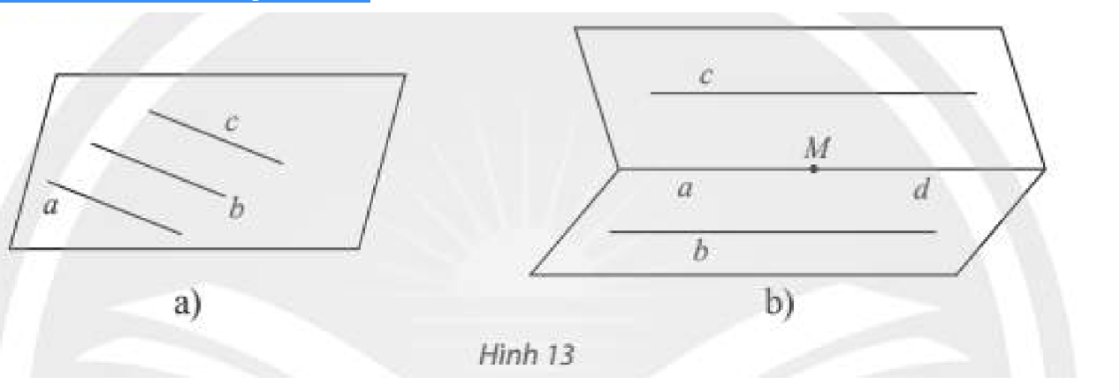
Cho hình chóp \(S.ABC\) và điểm thuộc miền trong tam giác \(ABC\) (Hình 17). Qua \(M\), vẽ đường thẳng \(d\) song song với \(SA\), cắt \(\left( {SBC} \right)\) tại \(N\). Trên hình vẽ, hãy chỉ rõ vị trí của điểm \(N\) và xác định giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {CMN} \right)\).