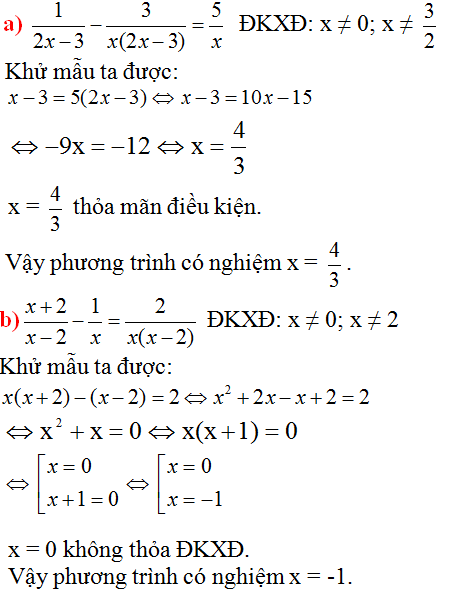(=)2x+3=x-5

(=)x+8=0

(=)x=-8

\(\left(2x+3\right)\left(\dfrac{3x+8}{2-7x}+1\right)=\left(x-5\right)\left(\dfrac{3x+8}{2-7x}+1\right)\)

ĐK: \(x\ne\dfrac{2}{7}\)

\(\Leftrightarrow\left(2x+3\right)\left(3x+8+2-7x\right)=\left(x-5\right)\left(3x+8+2-7x\right)\\ \Leftrightarrow\left(2x+3\right)\left(10-4x\right)=\left(x-5\right)\left(10-4x\right)\\ \Leftrightarrow\left(10-4x\right)\left(2x+3-x+5\right)=0\\ \Leftrightarrow\left(10-4x\right)\left(x+8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}10-4x=0\\x+8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\left(TM\right)\\x=-8\left(TM\right)\end{matrix}\right.\)

Vậy \(S=\left\{\dfrac{5}{2};-8\right\}\)

b: \(\Leftrightarrow\dfrac{7x+10}{x+1}\left(x^2-x-2-2x^2+3x+5\right)=0\)

\(\Leftrightarrow\left(7x+10\right)\left(-x^2+2x+3\right)=0\)

\(\Leftrightarrow\left(7x+10\right)\left(x^2-2x-3\right)=0\)

=>(7x+10)(x-3)=0

hay \(x\in\left\{-\dfrac{10}{7};3\right\}\)

d: \(\Leftrightarrow\dfrac{13}{2x^2+7x-6x-21}+\dfrac{1}{2x+7}-\dfrac{6}{\left(x-3\right)\left(x+3\right)}=0\)

\(\Leftrightarrow\dfrac{13}{\left(2x+7\right)\left(x-3\right)}+\dfrac{1}{\left(2x+7\right)}-\dfrac{6}{\left(x-3\right)\left(x+3\right)}=0\)

\(\Leftrightarrow26x+91+x^2-9-12x-14=0\)

\(\Leftrightarrow x^2+14x+68=0\)

hay \(x\in\varnothing\)

1/ ĐKXĐ : \(x\ne1\)

\(\dfrac{7x-3}{x-1}=\dfrac{2}{3}\)

\(\Leftrightarrow21x-9=2x-2\)

\(\Leftrightarrow19x=7\Leftrightarrow x=\dfrac{7}{19}\left(tm\right)\)

Vậy...

b/ \(\dfrac{2\left(3-7x\right)}{1+x}=\dfrac{1}{2}\) ĐKXĐ : \(x\ne-1\)

\(\Leftrightarrow12-28x=1+x\)

\(\Leftrightarrow11=29x\Leftrightarrow x=\dfrac{11}{29}\) \(\left(tm\right)\)

Vậy....

c/ ĐKXĐ : \(x\ne0\)

\(\dfrac{x^2-6}{x}=x+\dfrac{3}{2}\)

\(\Leftrightarrow\dfrac{x^2-6}{x}=\dfrac{2x+3}{2}\)

\(\Leftrightarrow2x^2-12=2x^2+3x\)

\(\Leftrightarrow3x=-12\Leftrightarrow x=-4\) \(\left(tm\right)\)

Vậy...

4/ ĐKXĐ : \(x\ne-\dfrac{2}{3}\)

\(\dfrac{5}{3x+2}=2x-1\)

\(\Leftrightarrow\left(2x-1\right)\left(3x+2\right)=5\)

\(\Leftrightarrow6x^2+4x-3x-2=5\)

\(\Leftrightarrow6x^2+x-7=0\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{7}{6}\\x=1\end{matrix}\right.\)

Vậy....

5,6 Tương tự nhé !

1)ĐKXĐ: \(x\ne1\)

Ta có: \(\dfrac{7x-3}{x-1}=\dfrac{2}{3}\)

\(\Leftrightarrow3\left(7x-3\right)=2\left(x-1\right)\)

\(\Leftrightarrow21x-9=2x-2\)

\(\Leftrightarrow21x-9-2x+2=0\)

\(\Leftrightarrow19x-7=0\)

\(\Leftrightarrow19x=7\)

\(\Leftrightarrow x=\dfrac{7}{19}\)(nhận)

Vậy: \(S=\left\{\dfrac{7}{19}\right\}\)

2) ĐKXĐ: \(x\ne-1\)

Ta có: \(\dfrac{2\left(3-7x\right)}{1+x}=\dfrac{1}{2}\)

\(\Leftrightarrow4\left(3-7x\right)=x+1\)

\(\Leftrightarrow12-28x-x-1=0\)

\(\Leftrightarrow-29x+11=0\)

\(\Leftrightarrow-29x=-11\)

\(\Leftrightarrow x=\dfrac{11}{29}\)

Vậy: \(S=\left\{\dfrac{11}{29}\right\}\)

3) ĐKXĐ: \(x\ne0\)

Ta có: \(\dfrac{x^2-6}{x}=x+\dfrac{3}{2}\)

\(\Leftrightarrow\dfrac{x^2-6}{x}=\dfrac{2x+3}{2}\)

\(\Leftrightarrow2\left(x^2-6\right)=x\left(2x+3\right)\)

\(\Leftrightarrow2x^2-12=2x^2+6x\)

\(\Leftrightarrow2x^2-12-2x^2-6x=0\)

\(\Leftrightarrow-6x-12=0\)

\(\Leftrightarrow-6x=12\)

\(\Leftrightarrow x=-2\)

Vậy: S={-2}

Giải:

a) \(8\left(3x-2\right)-13x=5\left(12-3x\right)+7x\)

\(\Leftrightarrow24x-16-13x=60-15x+7x\)

\(\Leftrightarrow24x-13x+15x-7x=60+16\)

\(\Leftrightarrow19x=76\)

\(\Leftrightarrow x=\dfrac{76}{19}=4\)

Vậy ...

b) \(\dfrac{5x}{x+2}-\dfrac{3}{x-2}+\dfrac{3x^2+6}{\left(x-2\right)\left(x+2\right)}=0\) (1)

ĐKXĐ: \(x\ne\pm2\)

\(\left(1\right)\Leftrightarrow\dfrac{5x\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{3x^2+6}{\left(x-2\right)\left(x+2\right)}=0\)

\(\Leftrightarrow5x\left(x-2\right)-3\left(x+2\right)+3x^2+6=0\)

\(\Leftrightarrow5x^2-10x-3x-6+3x^2+6=0\)

\(\Leftrightarrow8x^2-13x=0\)

\(\Leftrightarrow x\left(8x-13\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\8x-13=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(TM\right)\\x=\dfrac{13}{8}\left(TM\right)\end{matrix}\right.\)

Vậy ...

c) \(\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2x+2}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\) (2)

ĐKXĐ: \(x\ne-1;x\ne3\)

\(\left(2\right)\Leftrightarrow\dfrac{x\left(x+1\right)}{2\left(x-3\right)\left(x+1\right)}+\dfrac{x\left(x-3\right)}{2\left(x+1\right)\left(x-3\right)}=\dfrac{4x}{2\left(x+1\right)\left(x-3\right)}\)

\(\Leftrightarrow x\left(x+1\right)+x\left(x-3\right)=4x\)

\(\Leftrightarrow x\left(x+1+x-3\right)=4x\)

\(\Leftrightarrow x\left(2x-2\right)=4x\)

\(\Leftrightarrow2x-2=4\)

\(\Leftrightarrow x=3\)

Vậy ...

\(a,3-x=x+1,8\)

\(\Rightarrow-x-x=1,8-3\)

\(\Rightarrow-2x=-1,2\)

\(\Rightarrow x=0,6\)

\(b,2x-5=7x+35\)

\(\Rightarrow2x-7x=35+5\)

\(\Rightarrow-5x=40\)

\(\Rightarrow x=-8\)

\(c,2\left(x+10\right)=3\left(x-6\right)\)

\(\Rightarrow2x+20=3x-18\)

\(\Rightarrow2x-3x=-18-20\)

\(\Rightarrow-x=-38\)

\(\Rightarrow x=38\)

\(d,8\left(x-\dfrac{3}{8}\right)+1=6\left(\dfrac{1}{6}+x\right)+x\)

\(\Rightarrow8x-3+1=1+6x+x\)

\(\Rightarrow8x-3=7x\)

\(\Rightarrow8x-7x=3\)

\(\Rightarrow x=3\)

\(e,\dfrac{2}{9}-3x=\dfrac{4}{3}-x\)

\(\Rightarrow-3x+x=\dfrac{4}{3}-\dfrac{2}{9}\)

\(\Rightarrow-2x=\dfrac{10}{9}\)

\(\Rightarrow x=-\dfrac{5}{9}\)

\(g,\dfrac{1}{2}x+\dfrac{5}{6}=\dfrac{3}{4}x-\dfrac{1}{2}\)

\(\Rightarrow\dfrac{1}{2}x-\dfrac{3}{4}x=-\dfrac{1}{2}-\dfrac{5}{6}\)

\(\Rightarrow-\dfrac{1}{4}x=-\dfrac{4}{3}\)

\(\Rightarrow x=\dfrac{16}{3}\)

\(h,x-4=\dfrac{5}{6}\left(6-\dfrac{6}{5}x\right)\)

\(\Rightarrow x-4=5-x\)

\(\Rightarrow x+x=5+4\)

\(\Rightarrow2x=9\)

\(\Rightarrow x=\dfrac{9}{2}\)

\(k,7x^2-11=6x^2-2\)

\(\Rightarrow7x^2-6x^2=-2+11\)

\(\Rightarrow x^2=9\Rightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)

\(m,5\left(x+3\cdot2^3\right)=10^2\)

\(\Rightarrow5\left(x+24\right)=100\)

\(\Rightarrow x+24=20\)

\(\Rightarrow x=-4\)

\(n,\dfrac{4}{9}-\left(\dfrac{1}{6^2}\right)=\dfrac{2}{3}\left(x-\dfrac{2}{3}\right)^2+\dfrac{5}{12}\)

\(\Rightarrow\dfrac{2}{3}\left(x-\dfrac{2}{3}\right)^2+\dfrac{5}{12}=\dfrac{4}{9}-\dfrac{1}{36}\)

\(\Rightarrow\dfrac{2}{3}\left(x-\dfrac{2}{3}\right)^2+\dfrac{5}{12}=\dfrac{5}{12}\)

\(\Rightarrow\dfrac{2}{3}\left(x-\dfrac{2}{3}\right)^2=0\)

\(\Rightarrow x-\dfrac{2}{3}=0\Rightarrow x=\dfrac{2}{3}\)

#\(Urushi\text{☕}\)

a: 3-x=x+1,8

=>-2x=-1,2

=>x=0,6

b: 2x-5=7x+35

=>-5x=40

=>x=-8

c: 2(x+10)=3(x-6)

=>3x-18=2x+20

=>x=38

d; 8(x-3/8)+1=6(1/6+x)+x

=>8x-3+1=1+6x+x

=>8x-2=7x+1

=>x=3

e: =>-3x+x=4/3-2/9

=>-2x=12/9-2/9=10/9

=>x=-5/9

g: =>3/4x-1/2x=5/6+1/2

=>1/4x=5/6+3/6=8/6=4/3

=>x=4/3*4=16/3

h: =>x-4=-x+5

=>2x=9

=>x=9/2

\(i.\dfrac{\left(2x+1\right)^2}{5}-\dfrac{\left(x-1\right)^2}{3}=\dfrac{7x^2-14x-5}{15}\)

\(\Leftrightarrow\dfrac{4x^2+4x+1}{5}-\dfrac{x^2-2x+1}{3}=\dfrac{7x^2-14x-5}{15}\)

\(\Leftrightarrow\dfrac{12x^2+12x+3}{15}-\dfrac{5x^2-10x+5}{15}=\dfrac{7x^2-14x-5}{15}\)

\(\Leftrightarrow12x^2+12x+3-5x^2+10x-5=7x^2-14x-5\)

\(\Leftrightarrow36x=-3\)

\(\Leftrightarrow x=-\dfrac{1}{12}\)

\(k.x+\dfrac{2x+\dfrac{x-1}{5}}{3}=1-\dfrac{3x-\dfrac{1-2x}{3}}{5}\)

\(\Leftrightarrow\dfrac{15x}{15}+\dfrac{10x+x-1}{15}=\dfrac{15}{15}-\dfrac{9x-1+2x}{15}\)

\(\Leftrightarrow15x+9x-1=14-7x\)

\(\Leftrightarrow31x=15\)

\(\Leftrightarrow x=\dfrac{15}{31}\)

câu h tương tự bài trước câu g mik làm nhé