Cho tam giác đều ABC. Vẽ đường tròn tâm O, đường kính BC cắt AB và AC lần lượt tại D và E
a)So sánh DE và BC
b)Tam giác OBD là tam giác gì?vì sao?
c)Chứng Minh: DE//BC
Những câu hỏi liên quan
cho tam giác ABC nhọn. Vẽ đường tròn tâm O dường kính BC cắt 2 cạnh AB,AC lần lượt tại E và D; BD và CE cắt nhau tại H
a,chứng minh rằng: H vuông góc với BC
b,chứng minh: bốn điểm A,H,E,D cùng thuộc 1 đường tròn và DE<BC
c,gọi M,N lần lượt chân các đường vuông góc kẻ từ B và C đến DE. Chứng minh rằng ME=ND
a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại H
Do đó: AH⊥BC
Đúng 0
Bình luận (0)
Cho tam giác ABC có
B
A
C
^
45
0
, các góc B và C đều nhọn. Đường tròn đường kính BC cắt AB và AC lần lượt tai D và E. Gọi H là giao điểm của CD và BEa, Chứng minh AE BEb, Chứng minh tứ giác ADHE nội tiếp. Xác định tâm K của đường tròn ngoại tiếp tứ giác nàyc, Chứng minh OE là tiếp...
Đọc tiếp
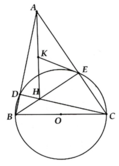
Cho tam giác ABC có B A C ^ = 45 0 , các góc B và C đều nhọn. Đường tròn đường kính BC cắt AB và AC lần lượt tai D và E. Gọi H là giao điểm của CD và BE
a, Chứng minh AE = BE
b, Chứng minh tứ giác ADHE nội tiếp. Xác định tâm K của đường tròn ngoại tiếp tứ giác này
c, Chứng minh OE là tiếp tuyến của đường tròn ngoại tiếp tam giác ADE
d, Cho BC = 2a. Tính diện tích viên phân cung D E ⏜ của đường tròn (O) theo a
a, HS tự chứng minh
b, HS tự chứng minh
c, DAEH vuông nên ta có: KE = KA = 1 2 AH
=> DAKE cân tại K
=> K A E ^ = K E A ^
DEOC cân ở O => O C E ^ = O E C ^
H là trực tâm => AH ^ BC
Có A E K ^ + O E C ^ = H A C ^ + A C O ^ = 90 0
(K tâm ngoại tiếp) => OE ^ KE
d, HS tự làm
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn (AB < AC) .Vẽ đường tròn (O; R) đường kính BC cắt hai cạnh AB, AC lần lượt tại E và D.Gọi H là giao điểm của BD và CE. a) Chứng minh: góc BEC = 90° và tứ giác AEHD nội tiếp b) Tia DE cắt đường thẳng BC tại S. Chứng minh: AH vuông góc BC và SE .SD=SB.SC c)Tia AH cắt BC tại F. Chứng minh: FEC =FAC và tứ giác OFED nội tiếp và OF.OS = R²
a: góc BEC=1/2*180=90 độ
góc BDC=1/2*180=90 độ
góc AEH+góc ADH=180độ
=>AEHD nội tiếp
b: Xet ΔABC có BD,CE là đường cao
BD cắt CE tại H
=>H là trực tâm
=>AH vuông góc BC
Xét ΔSBE và ΔSDC co
góc SBE=góc SDC
góc S chung
=>ΔSBE đồng dạngvơi ΔSDC
=>SB/SD=SE/SC
=>SB*SC=SD*SE
c: góc AFC=góc AEC=90 độ
=>AEFC nội tiếp
=>góc FEC=góc FAC
Đúng 1
Bình luận (0)
Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R, đường kính BC với AB < AC
a) tính góc BAC
b) Vẽ đường tròn tâm I, đường kính AO cắt AB, AC lần lượt tại H và K. Chứng minh H, I, K thẳng hàng
c) Tia OH, OK cắt tiếp tuyến tại A với đường tròn tâm O lần lượt tại D, E. Chứng minh BD + CE = DE
d) Chứng tỏ đường tròn đi qua 3 điểm D, O, E tiếp xúc với BC
a) Tam giác ABC nội tiếp đường tròn (O) đường kính BC
=> OA=OB=OC và O là trung điểm của BC
=> Tam giác ABC vuông tại A
=> góc BAC = 90 độ
b) DO tam giác HAK nội tiếp đường tròn (I)
Lại có góc HAK = 90 độ
=> HK là đường kính của (I)
=> HK đi qua I
=> H,I,K thẳng hàng
c) Đề bài ghi ko rõ
d) 3 điểm nào?
cho tam giác nhọn ABC. Vẽ đường tròn tâm O đường kính BC, đường tròn này cắt AB, AC lần lượt tại D và E. Biết sđ cung DE là 60 độa.Tính số đo góc A và số đo góc BHCb.Chứng minh:AD.AB=AE.AC
a) Xét (O) có
\(\widehat{DBE}\) là góc nội tiếp chắn \(\stackrel\frown{DE}\)
Do đó: \(\widehat{DBE}=\dfrac{1}{2}\cdot sđ\stackrel\frown{DE}\)(Định lí góc nội tiếp)
\(\Leftrightarrow\widehat{DBE}=\dfrac{1}{2}\cdot60^0=30^0\)
Xét (O) có
ΔBEC nội tiếp đường tròn(B,E,C∈(O))
BC là đường kính(gt)
Do đó: ΔBEC vuông tại E(Định lí)
⇒BE⊥CE tại E
hay BE⊥AC tại E
Ta có: ΔAEB vuông tại E(BE⊥AC tại E)
nên \(\widehat{EAB}+\widehat{ABE}=90^0\)(hai góc nhọn phụ nhau)
⇒\(\widehat{BAC}=90^0-\widehat{ABE}=90^0-30^0\)
⇒\(\widehat{BAC}=60^0\)
Vậy: \(\widehat{BAC}=60^0\)
Đúng 2
Bình luận (0)
Cho tam giác ABC nội tiếp đường tròn tâm O, đường phân giác của góc A và góc B cắt nhau tại I , cắt đường tròn tâm O lần lượt tại D và E, gọi E là giao điểm của AC và DE. Chứng minh :
a) DE là đường trung trực của IC
b) IF song song BC
Cho tam giác ABC nội tiếp đường tròn (O) đường kính BC. Kẻ đường cao AH của tam giác ABC. Biết BC=20cm, AH/AC= 3/4
1. Tính AB và AC
2. Đường tròn đường kính AH cắt (O), AB, AC lần lượt tại M,D,E. DE cắt BC tại K. Chứng minh: A,M,K thẳng hàng
3. Chứng minh: B, D, E, C cùng thuộc một đường tròn
Cho tam giác ABC nhọn vẽ đường tròn tâm O đường kính BC cắt tại AB và AC lần lượt tại D và E. Gọi H là giao điểm của BE và CD chứng minh H là trực tâm của tam giác ABC Từ đó suy ra AH vuông góc với BC
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>CD\(\perp\)DB tại D
=>CD\(\perp\)AB tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>BE\(\perp\)EC tại E
=>BE\(\perp\)AC tại E
Xét ΔABC có
BE,CD là đường cao
BE cắt CD tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC
Đúng 1
Bình luận (0)
cho tam giác ABC cân ở A, vẽ đường tròn tâm D đường kính BC cắt AB và AC lần lượt tại E và F. Các dây BF và CE cắt nhau ở H
a) AEHF thuộc 1 đường tròn, xác định tâm O
b) DE là tiếp tuyến của đường tròn tâm O
c) BC=10cm, AB=13cm. Tính bán kính đường tròn tâm O