2x - 7m + y = (2x + y) - 7m

Ta có: m = 2 => 7m = 7.2 = 14

Ta có: (2x + y) - 14

Thế 2x + y = 35 vào (2x + y) - 14 (hay 7m)

Ta được: 35 - 14 = 21

Vậy 2x - 7m + y = 21 khi 2x + y = 35 và m = 2

\(2x-7m+y=\left(2x+y\right)-7m=35-7.2=35-14=21\)

Trương Hồng Hạnh

Trần Quỳnh Mai

Nguyễn Thị Thu An

\(\left[1;-4\right]??\)

Xét trên \(\left[-1;2\right]\Rightarrow y=x^2-2x-8\) có \(-\dfrac{b}{2a}=1\)

\(y\left(-1\right)=-5;y\left(1\right)=-9;y\left(2\right)=-8\)

Xét trên \((2;4]\Rightarrow y=2x-12\)

\(y\left(4\right)=-4\)

So sánh các giá trị trên, ta được \(M=-4;m=-9\)

\(\Rightarrow M+m=-13\)

\(\hept{\begin{cases}2x+5y=7m+2\\2x+3y=m+2\end{cases}}\Rightarrow2y=6m\)

\(\hept{\begin{cases}2x+3y=m+2\\2x+y=5\end{cases}}\Rightarrow2y=m-3\)

\(\Rightarrow6m=m-3\Leftrightarrow m=-\frac{3}{5}\)

Thử lại thỏa mãn. 

a ) A = M + N = ( 2x²y - xy² + 3x - 2y ) + ( 2xy² - 2x²y - 5x + 2y )

                      =  2x²y - xy² + 3x - 2y + 2xy² - 2x²y - 5x + 2y 

                      =  ( 2x²y - 2x²y ) + ( -xy² + 2xy² ) + ( 3x - 5x ) + ( - 2y + 2y )

                      =   0 + ( -1 +2 ) xy² + ( 3 - 5 )x + 0

                      =  xy² - 2x

     Vậy A = M + N = xy² - 2x

    B = N - M =  2xy² - 2x²y - 5x + 2y - ( 2x²y - xy² + 3x - 2y )

                    =    2xy² - 2x²y - 5x + 2y - 2x²y + xy² - 3x + 2y 

                    =  ( 2xy² + xy² ) + ( -2x²y - 2x²y ) + ( - 5x - 3x ) + (  2y + 2y )

                    =  ( 2 + 1 )xy² + ( -2 - 2 )x²y  + ( - 5 - 3 )x  + (  2 + 2 )y 

                    =  3xy² - 4x²y  - 8x  + 4y 

 Vậy B = 3xy² - 4x²y  - 8x  + 4y 

Để (d)//(d') thì \(\left\{{}\begin{matrix}3-m=2\\m-5\ne3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m=1\\m\ne8\end{matrix}\right.\)

=>m=1

=>(d): y=(3-1)x+1-5=2x-4

Ta có: (d): y=2x-4; (d'): y=2x+3

Lấy A(3;2) thuộc (d)

=>KHoảng cách từ (d) đến (d') sẽ là khoảng cách từ A đến (d')

(d'): y=2x+3

=>2x-y+3=0

Khoảng cách từ A đến (d') là:

\(\dfrac{\left|2\cdot3+\left(-1\right)\cdot2+3\right|}{\sqrt{2^2+\left(-1\right)^2}}=\dfrac{7}{\sqrt{5}}=\dfrac{7\sqrt{5}}{5}\)

=>\(d\left(\left(d\right);\left(d'\right)\right)=\dfrac{7\sqrt{5}}{5}\)

Đáp án B

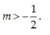
Để đường thẳng (d) vuông góc với đường thẳng  thì 2(3m + 2) = -1 hay:

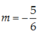
Chọn B.

\(a,Chu.vi:2.\left(2x+y+2x-y\right)=2.4x=8x\left(m\right)\\ b,Diện.tích:\left(2x+y\right)\left(2x-y\right)=\left(2x\right)^2-y^2=4x^2-y^2\left(m^2\right)\\ c,Thay:x=3;y=2.vào.biểu.thức.tính.diện.tích.thì.diện.tích.mảnh.vườn.là:\\ 4x^2-y^2=4.3^2-2^2=32\left(m^2\right)\)

a) Đa thức biểu thị chu vi mảnh vườn là:

\(2\cdot\left(2x+y+2x-y\right)=8x\left(m\right)\)

b) Đa thức biểu thị diện tích mảnh vườn là:

\(\left(2x+y\right)\left(2x-y\right)=4x^2-y^2\left(m^2\right)\)

c) Diện tích mảnh vườn khi \(x=3;y=2\) bằng:

\(4\cdot3^2-2^2\\=4\cdot9-4\\=36-4=32\)

a) Đa thức biểu thị chu vi hình chữ nhật là:

\(\left(2x+y+2x-y\right)\cdot2=4x\cdot2=8x\left(m\right)\)

b) Đa thức biểu thị diện tích hình chữ nhật là:

\(\left(2x+y\right)\left(2x-y\right)=\left(2x\right)^2-y^2=4x^2-y^2\left(m^2\right)\)

c) Diện tích của mảnh vườn là:

\(4\cdot3^2-2^2=32\left(m^2\right)\)