Chọn đáp án C.

Gọi M là trung điểm của BC: 

Do tam giác ABC đều nên tâm đường tròn nội tiếp tam giác ABC là trọng tâm, tâm đường tròn ngoại tiếp tam giác ABC

Áp dụng định lí Pytago vào tam giác ABM ta có:

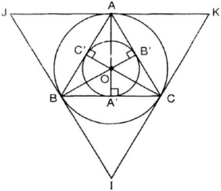
a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước thẳng và compa).

+ Dựng đoạn thẳng AB = 3cm .

+Dựng cung tròn (A, 3) và cung tròn (B, 3). Hai cung tròn này cắt nhau tại điểm C.

Nối A với C, B với C ta được tam giác đều ABC cạnh 3cm.

b) * Vẽ đường tròn:

Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực.

Dựng đường trung trực của đoạn thẳng BC và CA.

Hai đường trung trực cắt nhau tại O.

Vẽ đường tròn tâm O, bán kính OA = OB = OC ta được đường tròn ngoại tiếp tam giác ABC.

* Tính bán kính đường tròn.

+ Gọi A’ là trung điểm BC ⇒ A’C = BC/2 = a/2.

và AA’ ⊥ BC

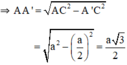
+ Do tam giác ABC là tam giác đều nên 3 đường trung trực đồng thời là ba đường trung tuyến

=> Giao điểm ba đường trung trực cũng là giao điểm ba đường trung tuyến

Suy ra O là trọng tâm tam giác ABC.

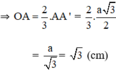
Vậy R = √3 (cm).

c) * Vẽ đường tròn:

Gọi A’; B’; C’ lần lượt là chân đường phân giác trong ứng với các góc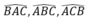 

Do tam giác ABC là tam giác đều nên A’; B’; C’ đồng thời là trung điểm BC; CA; AB.

Đường tròn (O; r) là đường tròn tâm O; bán kính OA’ = OB’ = OC’.

* Tính r:

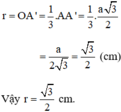
d) Vẽ các tiếp tuyến với đường tròn (O; R) tại A, B, C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ΔIJK là tam giác đều ngoại tiếp (O; R).

a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)

b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).

Ta có: R= OA = AA' = . = . = √3 (cm).

c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.

r = OA' = AA' = = (cm)

d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).

a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)

b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).

Ta có: R= OA = AA' = . = . = √3 (cm).

c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.

r = OA' = AA' = = (cm)

d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).

Chọn đáp án B.

Do O là tâm của đường tròn ngoại tiếp tam giác đều ABC nên O đồng thời là trọng tâm tam giác ABC.

Gọi M là trung điểm BC:

lx

lỗi 

a: góc OAD+góc OBD=180 độ

=>OADB nội tiếp

b: góc OAB+góc OBA=1/2*120=60 độ

=>góc AOB=120 độ

=>góc ADB=60 độ

=>CA=AD=DB=CB

=>CADB là hình thoi

hãy giúp tôi các bạn trẻ

Ta có :

Do BD và CE là các đường cao nên

suy ra góc BEC = góc BDC =90 độ

Xét tứ giác BCDE,có:

góc BEC=góc BDC

vậy BCDE là tứ giác nội tiếp(đpcm)

xet tu giac BCDE co:

goc BEC = BDC = 90 (vi BD va CE la cac duong cao)

⇒ tu giac bcde noi tiep (theo dau hieu nhan biet tu giac noi tiep) (dieu phai chung minh)

Đáp án là B