Quan sát đồ thị của hàm số \(y = \frac{1}{2}{x^2}\) ở Hình 4, hãy nêu nhận xét về vị trí cặp điểm E và H, F và G đối với trục Oy.

Hãy nhận xét một vài đặc điểm của đồ thị này bằng cách trả lời các câu hỏi sau (h.6):
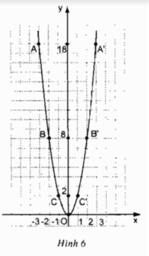
- Đồ thị nằm ở phía trên hay phía dưới trục hoành ?
- Vị trí của cặp điểm A, A’ đối với trục Oy ? Tương tự đối với các điểm B, B’ và C, C’ ?
- Điểm nào là điểm thấp nhất của đồ thị ?
Đồ thị nằm ở phía trên trục hoành
- Các cặp điểm A và A’; B và B’; C và C’ đối xứng nhau qua trục Oy
- Điểm O (0;0) là điểm thấp nhất của đồ thị.
Hãy nhận xét một vài đặc điểm của đồ thị này bằng cách trả lời các câu hỏi sau (h.6):
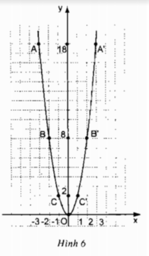
- Đồ thị nằm ở phía trên hay phía dưới trục hoành ?
- Vị trí của cặp điểm A, A’ đối với trục Oy ? Tương tự đối với các điểm B, B’ và C, C’ ?
- Điểm nào là điểm thấp nhất của đồ thị ?
Đồ thị nằm ở phía trên trục hoành
- Các cặp điểm A và A’; B và B’; C và C’ đối xứng nhau qua trục Oy
- Điểm O (0;0) là điểm thấp nhất của đồ thị.
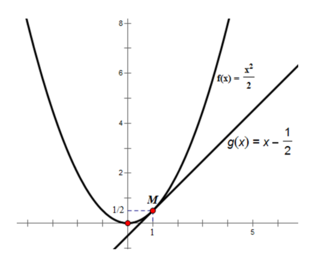
a) Vẽ đồ thị của hàm số f x = x 2 / 2 .
b) Tính f’(1).
c) Vẽ đường thẳng đi qua điểm M(1; 1/2) và có hệ số góc bằng f’(1). Nêu nhận xét về vị trí tương đối của đường thẳng này và đồ thị hàm số đã cho.
- Giả sử Δx là số gia của đối số tại xo = 1. Ta có:
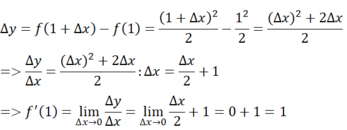
- Đường thẳng có hệ số góc bằng f'(1) = 1 có dạng:
y = 1.x + a hay y = x + a
Mà đường thẳng đó đi qua điểm M(1;1/2) nên có: 1/2 = 1 + a ⇒ a = 1/2 - 1 = -1/2
⇒ đường thẳng đi qua M và có hệ số góc bằng 1 là: y = x – 1/2
Ta có đồ thị như trên. Đường thẳng y = x – 1/2 tiếp xúc với đồ thị hàm số f(x) tại M
Quan sát đồ thị các hàm số: \(y = {x^2} - 4x + 3\) (Hình 14a);
\(y = \frac{{x + 1}}{{x - 1}}\,\,\left( {x \ne 1} \right)\) (Hình 14b);
\(y = \tan x\) (Hình 14c).
Và nêu nhận xét về tính liên tục của mỗi hàm số đó trên từng khoảng của tập xác định.
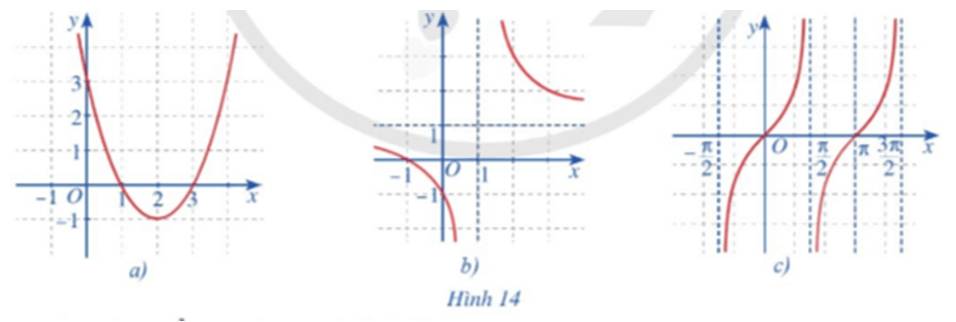
Hình 14a đồ thị là đường cong Parabol liền mạch nên hàm số liên tục trên toàn bộ trên khoảng xác định.
Hình 14b đồ thị bị chia làm hai nhánh:
- Với x < 1 ta thấy hàm số là một đường cong liền nên liên tục.
- Với x > 1 ta thấy hàm số là một đường cong liền nên liên tục.
Vậy hàm số liên tục trên từng khoảng xác định.
Hình 14c đồ thị hàm số y = tanx chia thành nhiều nhánh, và mỗi nhánh là các đường cong liền. Do đó hàm số liên tục trên mỗi khoảng xác định của chúng.
Xét hai hàm số \(y = {x^2},y = 2x\) và đồ thị của chúng trong Hình 2. Đối với mỗi trường hợp, nêu mối liên hệ của giá trị hàm số tại 1 và -1, 2 và -2. Nhận xét về tính đối xứng của mỗi đồ thị hàm số.
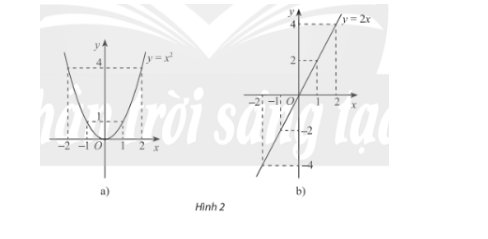
* Hàm số \(y = {x^2}\)
Nhìn đồ thị ta thấy:
+ \(y(1) = y( - 1) = 1,y(2) = y( - 2) = 4\)
+ Đồ thị hàm số đối xứng qua trục Oy.
* Hàm số \(y = 2x\)
Nhìn đồ thị ta thấy:
+ \(y(1) = - y( - 1),y(2) = - y( - 2)\)
+ Đồ thị hàm số đối xứng qua điểm O.
Quan sát giao điểm:
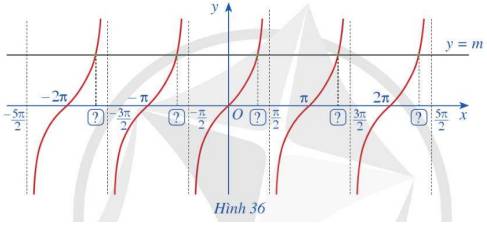
a) Từ hoành độ giao điểm của đồ thị hàm số y = tanx và đường thẳng y = m trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), hãy xác định tất cả các hoành độ giao điểm của hai đồ thị đó
b) Có nhận xét gì về nghiệm của phương trình tanx = m
a) Do hoành độ giao điểm nằm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) nên: \(\tan x = m \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \)
b) Nhận xét: trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), với mọi \(m \in \mathbb{R}\) ta luôn có \(x = \alpha + k\pi \)
Quan sát Hình 6.2 và cho biết những điểm nào sau đây nằm trên đồ thị của hàm số \(y=\dfrac{1}{2}x^2\).
\(\left(0;0\right);\left(2;2\right);\left(-2;2\right);\left(1;2\right);\left(-1;2\right)\)
Nêu nhận xét về mối quan hệ giữa hoành độ và tung độ của những điểm nằm trên đồ thị.
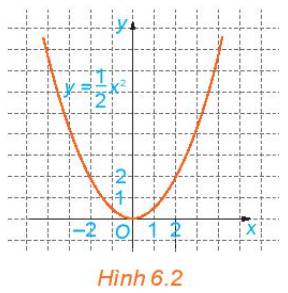
Dựa vào độ thị ta thấy (0; 0); (2; 2); (-2; 2) nằm trên đồ thị hàm số \(y = \frac{1}{2}{x^2}\)
Ta nhận ra được: \(\begin{array}{l}0 = \frac{1}{2}{.0^2}\\2 = \frac{1}{2}{.2^2}\\2 = \frac{1}{2}.{( - 2)^2}\end{array}\) Vì vậy những điểm có tọa độ \(\left( {x;\frac{1}{2}{x^2}} \right)\) sẽ nằm trên đồ thị.
Cho hàm số f(x)=x+1với x∈R.
a) Giả sử x0∈R.Hàm số f(x)
có liên tục tại điểm x0 hay không?
b) Quan sát đồ thị hàm số f(x)=x+1 với x∈R (Hình 13), nếu nhận xét về đặc điểm của đồ thị hàm số đó.
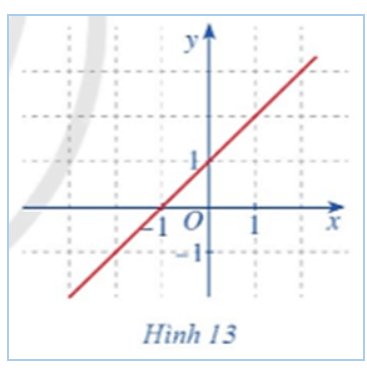
a: f(x0)=x0+1
\(\lim\limits_{x\rightarrow x0}f\left(x\right)=x_0+1\)=f(x0)
=>HS f(x) liên tục tại điểm x0
b: Đồ thị hàm số là một đường thẳng liền mạch với mọi x thực
Xét hàm số \(y = f\left( x \right) = \frac{{2{x^2} - 2}}{{x - 1}}\).
a) Bảng sau đây cho biết giá trị của hàm số tại một số điểm gần điểm 1.
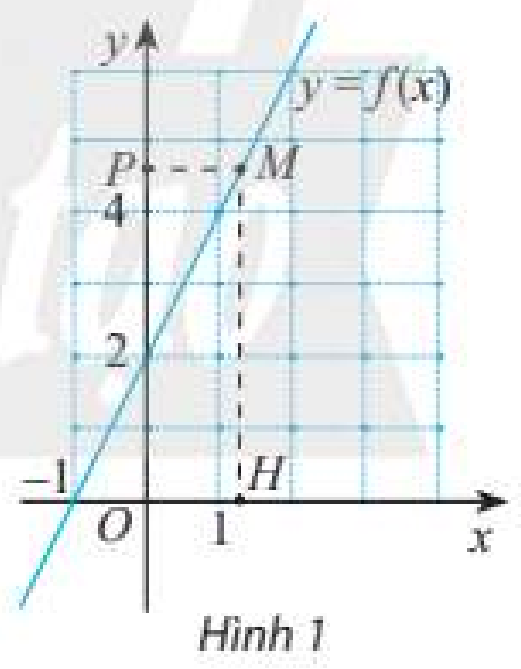
a) Khi \(x\) càng gần đến 1 thì giá trị của hàm số càng gần đến 4.
b) Khi điểm \(H\) thay đổi gần về điểm \(\left( {1;0} \right)\) trên trục hoành thì điểm \(P\) càng gần đến điểm \(\left( {0;4} \right)\).
Quan sát đồ thị \(y = \cos x\) ở Hình 28
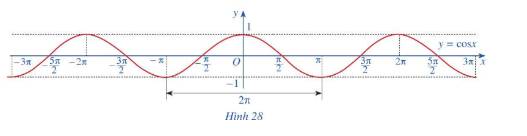
a) Nêu tập giá trị của hàm số \(y = \cos x\)
b) Trục tung có là trục đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số \(y = \cos x\)
c) Bằng cách dịch chuyển đồ thị \(y = \cos x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị có hàm số \(y = \cos x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\) hay không? Hàm số \(y = \cos x\) có tuần hoàn hay không?
d) Tìm khoảng đồng biến, nghịch biến của hàm số \(y = \cos x\)
a) Tập giá trị của hàm số \(y = \cos x\)là \(\left[ { - 1;1} \right]\)
b) Trục tung là trục đối xứng của hàm số \(y = \cos x\).
Như vậy hàm số \(y = \cos x\)là hàm số chẵn.
c) Bằng cách dịch chuyển đồ thị \(y = \cos x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị có hàm số \(y = \cos x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)
Như vậy hàm số \(y = \cos x\) là hàm số tuần hoàn
d) Hàm số \(y = \cos x\)đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\) với \(k \in Z\)