a) Khi \(x\) càng gần đến 1 thì giá trị của hàm số càng gần đến 4.
b) Khi điểm \(H\) thay đổi gần về điểm \(\left( {1;0} \right)\) trên trục hoành thì điểm \(P\) càng gần đến điểm \(\left( {0;4} \right)\).
a) Khi \(x\) càng gần đến 1 thì giá trị của hàm số càng gần đến 4.
b) Khi điểm \(H\) thay đổi gần về điểm \(\left( {1;0} \right)\) trên trục hoành thì điểm \(P\) càng gần đến điểm \(\left( {0;4} \right)\).
Cho hàm số \(f\left( x \right) = \frac{1}{{x - 1}}\) có đồ thị như Hình 4.
x
1,1
1,01
1,001
1,0001
y = f(x)
10
100
?
?
Từ đồ thị và bảng trên, có nhận xét gì về giá trị \(f\left( x \right)\) khi \(x\) dần tới 1 phía bên phải?
b) Tìm các giá trị còn thiếu trong bảng sau:
x | 0,9 | 0,99 | 0,999 | 0,9999 |
y = f(x) | – 10 | – 100 | ? | ? |
Từ đồ thị và bảng trên, có nhận xét gì về giá trị \(f\left( x \right)\) khi \(x\) dần tới 1 phía bên trái?
Giá cước vận chuyển bưu kiện giữa hai thành phố do một đơn vị cung cấp được cho bởi bảng sau:
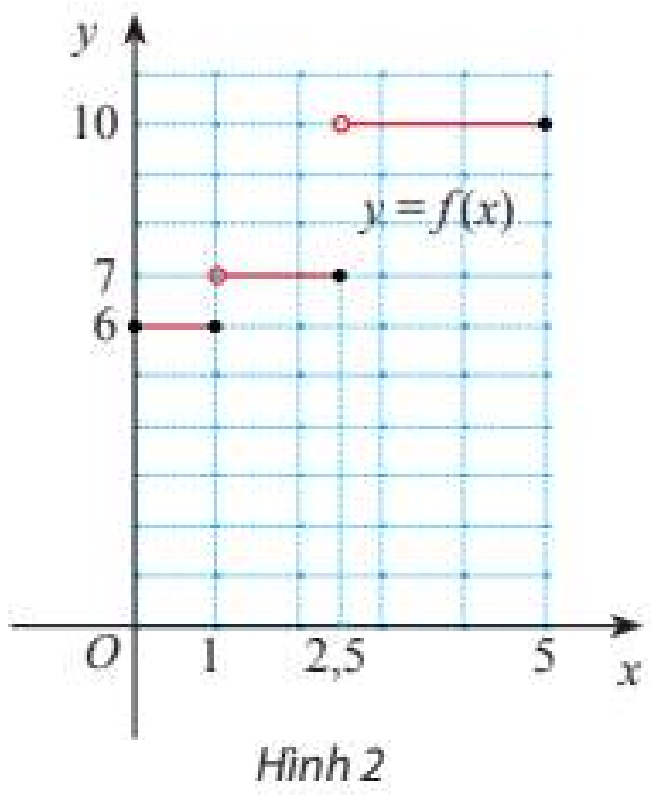
a) Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì sao cho \(x \in \left( {1;2,5} \right)\) và \(\lim {x_n} = 1\). Tìm \(\lim f\left( {{x_n}} \right)\).
b) Giả sử \(\left( {{x_n}'} \right)\) là dãy số bất kì sao cho \({x_n}' \in \left( {0;1} \right)\) và \(\lim {x_n}' = 1\). Tìm \(\lim f\left( {{x_n}'} \right)\).
c) Nhận xét về kết quả ở a) và b)
Cho hai hàm số và \(y = g\left( x \right) = \frac{x}{{x + 1}}\).
a) Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thoả mãn \({x_n} \ne - 1\) với mọi \(n\) và \({x_n} \to 1\) khi \(n \to + \infty \). Tìm giới hạn \(\lim \left[ {f\left( {{x_n}} \right) + g\left( {{x_n}} \right)} \right]\).
b) Từ đó, tìm giới hạn \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right]\), và so sánh với \(\mathop {\lim }\limits_{x \to 1} {\rm{ }}f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right)\).
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{1 - 2x}&{khi\,\,x \le - 1}\\{{x^2} + 2}&{khi\,\,x > - 1}\end{array}} \right.\).
Tìm các giới hạn \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to - {1^ - }} {\rm{ }}f\left( x \right)\) và \(\mathop {\lim }\limits_{x \to - 1} f\left( x \right)\) (nếu có).
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{ - {x^2}}&{khi\,\,x < 1}\\x&{khi\,\,x \ge 1}\end{array}} \right.\).
Tìm các giới hạn \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right);\mathop {\lim }\limits_{x \to {1^ - }} {\rm{ }}f\left( x \right);\mathop {\lim }\limits_{x \to 1} f\left( x \right)\) (nếu có).
Cho hàm số \(f\left( x \right) = \frac{1}{x}\) có đồ thị như Hình 3.

a) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, nêu nhận xét về giá trị \(f\left( x \right)\) khi \(x\) càng lớn (dần tới \( + \infty \))?
b) Tìm các giá trị còn thiếu trong bảng sau:
x | – 100 000 | – 10 000 | – 1 000 | – 100 | – 10 |
y = f(x) | ? | ? | ? | –0,01 | –0,1 |
Từ đồ thị và bảng trên, nêu nhận xét về giá trị \(f\left( x \right)\) khi \(x\) càng bé (dần tới \( - \infty \))?
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to - 2} \left( {{x^2} + 5x - 2} \right)\);
b) \(\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x - 1}}\).
Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to 3} \left( {2{x^2} - x} \right)\);
b) \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} + 2x + 1}}{{x + 1}}\).
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to - 2} \left( {{x^2} - 7x + 4} \right)\)
b) \(\mathop {\lim }\limits_{x \to 3} \frac{{x - 3}}{{{x^2} - 9}}\)
c) \(\mathop {\lim }\limits_{x \to 1} \frac{{3 - \sqrt {x + 8} }}{{x - 1}}\)