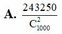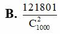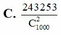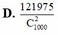Trong các hoạt động sau, hoạt động nào là phép thử ngẫu nhiên? Tại sao?
a) Chọn ra lần lượt hai tấm thẻ từ hộp có hai tấm thẻ như Hình 3a
b) Chọn bất kì 1 quyển sách từ giá như Hình 3b
c) Chọn 1 cây bút chì từ ống bút như Hình 3c.

Hộp thứ nhất đựng 1 thẻ xanh, 1 thẻ đỏ và 1 thẻ vàng. Hộp thứ hai đựng 1 thẻ xanh, 1 thẻ đỏ. Các tấm thẻ có kích thước có khối lượng như nhau. Lần lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ
a) Sử dụng sơ đồ hình cây, hãy liệt kê tất cả các kết quả có thể xảy ra
b) Tính xác suất của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ”
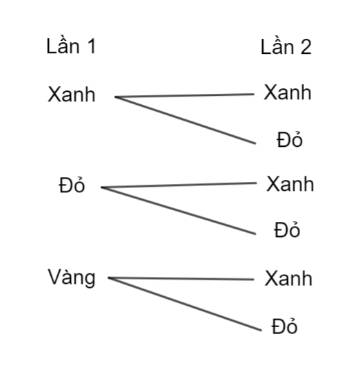
a) Các kết quả có thể xảy ra trong 2 lần lấy tấm thẻ từ 2 hộp được thể hiện ở sơ đồ hình cây như hình dưới đây:
b)
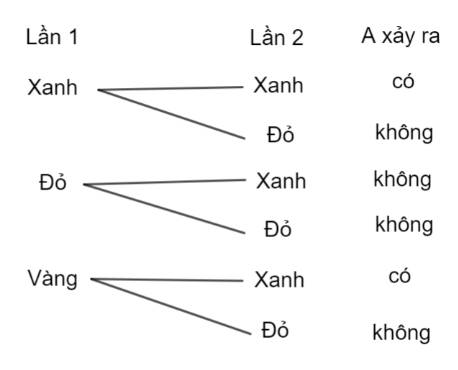
Gọi A là biến cố “Trong 2 thẻ lấy ra không có thẻ màu đỏ nào” là biến cố đối của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ”
Dựa vào sơ đồ hình cây ta thấy có tất cả 6 kết quả có thể xảy ra, trong đó có 2 kết quả thuận lợi cho I. Do đó: \(P(A) = \frac{2}{6} = \frac{1}{3}\)
Vậy xác suất của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ” là \(1 - \frac{1}{3} = \frac{2}{3}\)
Hãy trả lời câu hỏi ở Hoạt động mở đầu.
Trong hộp có 5 tấm thẻ cùng loại được đánh số lần lượt từ 1 đến 5. Lấy ra ngẫu nhiên lần lượt 2 thẻ từ hộp. Gọi \(A\) là biến cố “Thẻ lấy ra lần thứ nhất ghi số chẵn”; \(B\) là biến cố “Thẻ lấy ra lần thứ hai ghi số chẵn” và \(C\) là biến cố “Tích các số ghi trên hai thẻ lấy ra là số chẵn”.
Hãy viết tập hợp mô tả các biến cố trên.
THAM KHẢO:
A = {(2;1);(2;2);(2;3);(2;4);(2;5);(4;1);(4;2);(4;3);(4;4);(4;5)}
B = {(1;2);(2;2);(3;2);(4;2);(5;2);(1;4);(2;4);(3;4);(4;4);(5;4)}
C = {(1;2);(1;4);(2;1);(2;2);(2;3);(2;4);(2;5);(3;2);(3;4);(4;1);(4;2);(4;3);(4;4);(4;5); (5;2);(5;4)}
Có 20 tấm thẻ được đánh số từ 1 đến 20 .Chọn ngẫu nhiên ra 6 tấm thẻ. Xác suất để trong 6 tấm thẻ chọn ra có hai tấm thẻ mà tổng của hai số trên hai tấm thẻ đó bằng 21 là:
A. 56/323
B. 211/323
C. 112/323
D. 267/323
Một hộp chứa 10 tấm thẻ cùng loại được đánh số lần lượt từ 3 đến 12. Chọn ngẫu nhiên 1 tấm thẻ từ hộp. Hãy liệt kê các kết quả làm cho các biến cố sau xảy ra.
\(A\):” Số ghi trên thẻ lấy ra chia hết cho 3”.
\(B\):” Số ghi trên thẻ lấy ra chia hết cho 6”.
Khi lấy 1 tấm thẻ ra khỏi hộp thì số chỉ trên tấm thẻ có thể là: thẻ 3; thẻ 4; thẻ 5; thẻ 6; thẻ 7; thẻ 8; thẻ 9; thẻ 10; thẻ 11; thẻ 12.
Các kết quả cho biến cố \(A\): “ Số ghi trên thẻ lấy ra chia hết cho 3” là thẻ 3; thẻ 3; thẻ 9; thẻ 12.
Các kết quả cho biến cố \(B\): “ Số ghi trên thẻ lấy ra chia hết cho 6” là thẻ 6; thẻ 12.
Có 9 tấm thẻ đánh số từ 1 đến 9. Chọn ngẫu nhiên ra hai tấm thẻ. Tính xác suất để tích của hai số trên hai tấm thẻ là một số chẵn.
A. 13 18
B. 55 56
C. 5 28
D. 1 56
Có 9 tấm thẻ đánh số từ 1 đến 9. Chọn ngẫu nhiên ra hai tấm thẻ. Tính xác suất để tích của hai số trên hai tấm thẻ là một số chẵn
A. 13 18 .
B. 55 56 .
C. 5 28 .
D. 1 56 .
Chọn A.
Lấy ngẫu nhiên tấm thẻ từ 9 tấm thẻ có C 9 2 = 36 cách => số phần tử của không gian mẫu là n Ω = 36 .
Gọi A: “tích của hai số trên tấm thẻ là một số chẵn”.
Để tích của hai số trên tấm thẻ là một số chẵn thì ít nhất một trong hai tấm thẻ phải là số chẵn. Ta có hai trường hợp
TH1: Cả hai thẻ được lấy ra đều là số chẵn có C 4 2 = 6 cách.
Th2: Hai thẻ lấy ra có một thẻ là số chẵn, một thẻ là số lẻ C 4 1 . C 5 1 = 20 cách.
Số kết quả thuận lợi cho A là n(A) = 6 + 20 = 26.
Vậy xác suất của biến cố A là P A = n A n Ω = 13 18 .
Một hộp có 10 tấm thẻ giống nhau được đánh số lần lượt từ 1 đến 10. Chọn ngẫu nhiên cùng lúc 3 thẻ. Tính xác suất của biến cố “Tích các số ghi trên ba thẻ đó là số chẵn”.
Do các tấm thẻ giống nhau, nên lấy 3 tấm từ 10 tấm không quan tâm thứ tự có \(C_{10}^3 = 120\)cách, suy ra \(n\left( \Omega \right) = 120\)
Gọi A là biến cố “Tích các số ghi trên ba thẻ đó là số chẵn”
Để tích các số trên thẻ là số chẵn thì ít nhất có 1 thẻ là số chẵn
Để chọn ra 3 thẻ thuận lợi cho biến cố A ta có 3 khả năng
+) Khả năng 1: 3 thẻ chọn ra có 1 thẻ có số chẵn và 2 thẻ có số lẻ có \(5.C_5^2 = 50\) khả năng
+) Khả năng 2: 3 thẻ chọn ra có 2 thẻ có số chẵn và 1 thẻ có số lẻ có \(C_5^2.5 = 50\) khả năng
+) Khả năng 3: 3 thẻ chọn ra có đều là có số chắn có \(C_5^3 = 10\) khả năng
Suy ra \(n\left( A \right) = 50 + 50 + 10 = 110\)
Vậy xác suất của biến cố A là: \(P(A) = \frac{{110}}{{120}} = \frac{{11}}{{12}}\)
Hộp thứ nhất chứa 3 tấm thẻ cùng loại được đánh số lần lượt từ 1 đến 3. Hộp thứ hai chứa 5 tấm thẻ cùng loại được đánh số lần lượt từ 1 đến 5. Lấy ra ngẫu nhiên từ mỗi hộp 1 thẻ. Gọi \(A\) là biến cố “Tổng các số ghi trên 2 thẻ bằng 6”, \(B\) là biến cố “Tích các số ghi trên 2 thẻ là số lẻ”.
a) Hãy viết tập hợp mô tả biến cố \(AB\) và tính \(P\left( {AB} \right)\).
b) Hãy tìm một biến cố khác rỗng và xung khắc với cả hai biến cố \(A\) và \(B\).
a) Tập hợp mô tả biến cố AB:
`AB: { (1, 5), (2, 4), (3, 3) }`
P(AB) = số phần tử trong AB / số phần tử trong không gian mẫu
`P(AB) = 3 / (3 * 5) = 3/15 = 1/5`
b) Một biến cố khác rỗng và xung khắc với cả hai biến cố A và B là biến cố "Tổng các số ghi trên 2 thẻ lớn hơn 6".
$HaNa$
có 20 tấm thẻ được đánh số từ 1 đến 20 Chọn ngẫu nhiên ra 6 Tấm thẻ xác suất để trong 6 tấm thẻ chọn ra hai tấm thẻ mà tổng của hai số thẻ trên hai tấm thẻ đó bằng 21 là
Lời giải:
Gọi $Q$ là tập hợp tất cả các cách lấy ra $6$ tấm thẻ trong số $20$ tấm thẻ. Ta có: $|Q|=C^6_{20}$
Gọi $A$ là biến cố trong 6 tấm thẻ có 2 tấm thẻ có tổng bằng $21$.
Các cặp số có tổng là $21$ là: $(1,20); (2,19); (3,18);...; (10;11)$ (10 cặp). 4 số còn lại ta có $C^4_{18}$ cách chọn.
Do đó số khả năng để trong 6 số có 2 số có tổng bằng $21$ là: $10.C^4_{18}$
Do đó xác suất để xảy ra biến cố A là: $\frac{10.C^4_{18}}{C^6_{20}}=\frac{15}{19}$
Từ một hộp có 1000 thẻ được đánh số từ 1 đến 1000. Chọn ngẫu nhiên ra hai thẻ. Tính xác suất để chọn được hai thẻ sao cho tổng của các số ghi trên hai thẻ nhỏ hơn 700.