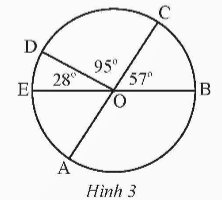
Tính số đo góc ở tâm \(\widehat {EOA}\) và \(\widehat {AOB}\) trong Hình 3. Biết AC và BE là hai đường kính của đường tròn (O).
Những câu hỏi liên quan
Cho đường tròn tâm $O$, đường kính $AD = 2R$. Vẽ dây cung tâm $D$ bán kính $R$, cung này cắt đường tròn $(O)$ ở $B$ và $C$.
a) Tứ giác $OBDC$ là hình gì? Vì sao?
b) Tính số đo các góc \(\widehat{CBD};\widehat{CBO};\widehat{OBA}\)
c) Chứng minh tam giác $ABC$ là tam giác đều.
cho đường tròn tâm O và một điểm M nằm ngoài đường tròn . Qua M vẽ các tiếp tuyến MA,MB với đường tròn tâm O . Biết \(\widehat{AMB}\) = 54 độ . Hỏi 2 bán kính OA,OB tạo thành góc ở tâm \(\widehat{AOB}\) bằng bao nhiêu độ
Hình bạn tự vẽ nhé :
Xét tứ giác OAMB có : góc AOB + góc OAM + góc AMB +góc OBM =360 độ
⇒ góc AOB + 90 độ +54 độ +90 độ =360 độ
⇒ góc AOB =360 độ - 90 độ -90 độ -54 độ = 126 độ
Đúng 1
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB=2R (R>9). Trên bán kính OA lấy hai điểm C và D sao cho AC=6; AD=9. Đường thẳng vuông góc với AB tại D cắt nửa đường tròn tại E. Điểm F thuộc nửa đường tròn sao cho \(\widehat{ACF}=\widehat{DCE}\). Đường tròn tâm I bán kính r tiếp xúc với 2 cạnh của góc ECF và tiếp xúc trong với đường tròn tâm O. Tính r.
Giải mục 1 trang 7 ,8 , 9 SGK Toán 11 tập 1 - Chân trời sáng tạo
16 tháng 7 2023 lúc 16:41
Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được một cung AB có độ dài đúng bằng R (Hình 9). Đo và cho biết \(\widehat {AOB}\) có số đo bằng bao nhiêu độ.
\( \Rightarrow \widehat {AOB} = 60^\circ \)
Đúng 1
Bình luận (0)
Giả sử M là một điểm nằm ngoài đường tròn (O ; R) . Từ M kẻ hai tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Biết rằng OM = 2R, tìm số đo góc ở tâm $\widehat{AOB}$.
Gọi I là trung điêm OM
do đó ta có tính chất của trung tuyến ứng với cạnh huyền lầ
\(IO=IA=IM=\frac{1}{2}OM=\frac{1}{2}.2R=R\)
Xét tam giác IOA có \(IO=OA=AI=R\Rightarrow\)tam giác IOA đều nên IOA = 60 độ
chứng minh tương tự ta sẽ có góc IOB=60 độ
nên AOB=AOI+IOB=120 độ
Vì MA , MB lần lượt là các tiếp tuyến tại A , B của đường tròn (O) => góc MAO = góc MBO = 90 độ
tam giác MAO vuông tại A có R=OA=1/2 OM => góc AMO = 30 độ
tương tự góc OMB = 30 độ
tứ giác OAMB có góc OAM+OBM+AMO+BMO+AOB=360 độ
=> góc AOB =120 độ
Xem thêm câu trả lời
Hai tiếp tuyến của đường tròn (O) tại A và B cắt nhau tại M. Biết \(\widehat{AMB}=35^o.\)
a) Tính số đo của góc ở tâm tạo bở hai bán kính OA, OB.
b) Tính số đo mỗi cung AB (cung lớn và cung nhỏ).
a) Trong tứ giác AOBM có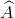 
= 
= 
.
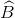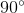Suy ra cung AMB + 
= 
=> cung AMB= -
= - 
= 
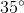
b) Từ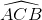 
= . Suy ra số đo cung nhỏ AB = và số đo cung lớn AB :
Cung AB =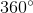 
- = 
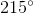
Đúng 0
Bình luận (0)
cho đường tròn tâm O đường kính AB .Vẽ góc ở tâm \(\widehat{AOC}\) =50 độ . Vẽ dây CD \(\perp\)AB và dây DE//AB
a)Tính số đo cung nhỏ BE
b)Tính số đo \(\stackrel\frown{CBE}\) từ đó suy ra 3 điểm C,O,E thẳng hàng
Tự vẽ hình
a) Do \(CD\) vuông góc \(AB\) nên \(AB\) là trung trực của \(CD\) (liên hệ giữa đường kính và dây cung)
\(\Rightarrow AC=AD\Rightarrow sđ\stackrel\frown{AC}=sđ\stackrel\frown{AD}\)
Mà \(sđ\stackrel\frown{AC}=\stackrel\frown{AOC}=50^0\Rightarrow sđ\stackrel\frown{AD}=50^0\).
Do \(DE\) song song \(AB\)
\(sđ\stackrel\frown{BE}=sđ\stackrel\frown{AD}=50^0\Rightarrow\widehat{BOE}=sđ\stackrel\frown{BE}=50^0\).
b) Do \(B\in\stackrel\frown{CE}\Rightarrow sđ\stackrel\frown{CBE}=sđ\stackrel\frown{CB}+sđ\stackrel\frown{BE}\)
\(\Rightarrow sđ\stackrel\frown{CBE}=\widehat{COB}+\widehat{BOE}=180^0-\widehat{AOC}+\widehat{BOE}\)
\(\Rightarrow sđ\stackrel\frown{CBE}=180^0-50^0+50^0=180^0\)
\(\Rightarrow\) CE là đường kính
\(\Rightarrow\) C, O, E thẳng hàng.
Đúng 2
Bình luận (0)
Cho nửa đường tròn đường kính AB, tâm O. Đường tròn tâm A bán kính AO cắt nửa đường tròn đã cho tại C. Đường tròn tâm B bán kính BO cắt nửa đường tròn đã cho tại D. Đường thẳng qua O và song song với AD cắt nửa đường tròn đã cho tại E
a) widehat{ADC} và widehat{ABC} có bằng nhau không ? Vì sao ?
b) Chứng minh CD song song với AB
c) Chứng minh AD vuông góc với OC
d) Tính số đo của widehat{DAO}
e) So sánh hai cung BE cà CD
Đọc tiếp
Cho nửa đường tròn đường kính AB, tâm O. Đường tròn tâm A bán kính AO cắt nửa đường tròn đã cho tại C. Đường tròn tâm B bán kính BO cắt nửa đường tròn đã cho tại D. Đường thẳng qua O và song song với AD cắt nửa đường tròn đã cho tại E
a) \(\widehat{ADC}\) và \(\widehat{ABC}\) có bằng nhau không ? Vì sao ?
b) Chứng minh CD song song với AB
c) Chứng minh AD vuông góc với OC
d) Tính số đo của \(\widehat{DAO}\)
e) So sánh hai cung BE cà CD
2 tháng 4 2022 lúc 20:28
Cho \(\Delta ABC\) có ba góc nhọn nội tiếp đường tròn (O;R), AD là đường cao của \(\Delta ABC\) và AM là đường kính của đường tròn tâm O, gọi E là hình chiếu của B trên AM.
a) CM: \(\widehat{ACM}=90^o\) và \(\widehat{BAD}=\widehat{MAC}\)
b) CM: Tứ giác ABDE nội tiếp
c) CM: DE//BC
a: góc ACM=1/2*sđ cung AM=90 độ
góc BAD+góc ABD=90 độ
góc MAC+góc AMC=90 độ
mà góc ABD=góc AMC
nên góc BAD=góc MAC
b: góc AEB=góc ADB=90 độ
=>AEDB nội tiếp
Đúng 0
Bình luận (0)
Hình viên phân là phần hình tròn giới hạn bởi một cung và dây căng cung ấy. Hãy tính diện tích hình viên phân AmB, biết góc ở tâm \(\widehat{AOB}=60^o\) và bán kính đường tròn là 5,1 cm.
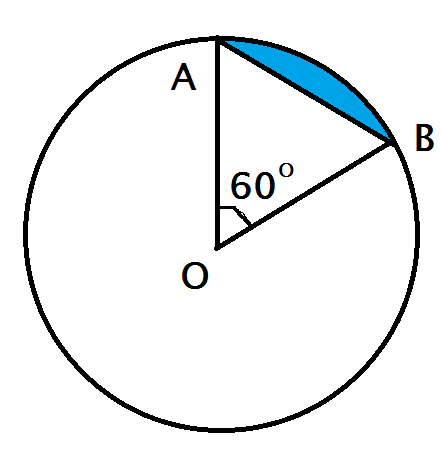
Hướng dẫn giải:
∆OAB là tam giác đều có cạnh bằng R = 5,1cm. Áp dụng công thức tính diện tích tam giác đều cạnh a là a2√44 ta có
S∆OBC = SΔOBC=R2√34 (1)
Diện tích hình quạt tròn AOB là:
π.R2.6003600=πR26 (2)
Từ (1) và (2) suy ra diện tích hình viên phân là:
πR26−R2√34=R2(π6−√34)
Thay R = 5,1 ta có Sviên phân ≈ 2,4 (cm2)
Đúng 0
Bình luận (0)