
\( \Rightarrow \widehat {AOB} = 60^\circ \)

\( \Rightarrow \widehat {AOB} = 60^\circ \)
Trong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính bằng 1 và điểm A(1; 0).
a) Cho điểm B(0; 1). Số đo góc lượng giác (OA; OB) bằng bao nhiêu radian?
b) Xác định các điểm A’ và B’ trên đường tròn sao cho các góc lượng giác (OA; OA’), (OA, OB’) có số đo lần lượt là \(\pi \,\) và \( - \frac{\pi }{2}\)
Hải lí là một đơn vị chiều dài hàng hải, được tính bằng độ dài một cung chắn một góc \(\alpha = {\left( {\frac{1}{{60}}} \right)^\circ }\) của đường kinh tuyến (Hình 17). Đổi số đo \(\alpha \) sang radian và cho biết 1 hải lí bằng khoảng bao nhiêu kilomet, biết bán kính trung bình của Trái Đất là 6371km. Làm tròn kết quả đến hàng phần trăm.
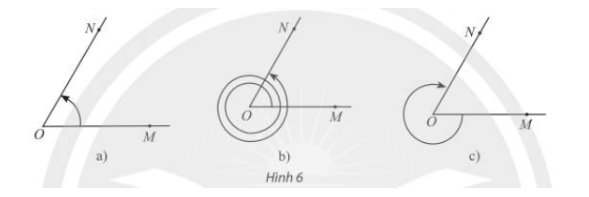
Cho \(\widehat {MON} = {60^ \circ }\). Xác định số đo của các góc lượng giác được biểu diễn trong Hình 6 và viết công thức tổng quát của số đo góc lượng giác (OM,ON).
Biểu diễn trên đường tròn lượng giác các góc lượng giác có số đo là:
a) \( - {1485^ \circ }\)
b) \(\frac{{19\pi }}{4}\)
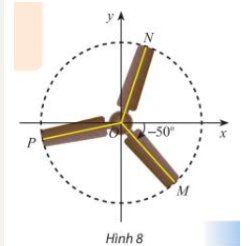
Trong Hình 8, chiếc quạt có ba cánh được phân bố đều nhau. Viết công thức tổng quát số đo của góc lượng giác (Ox,ON) và (Ox,OP).
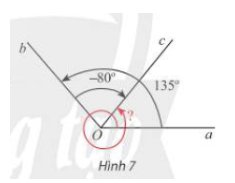
Cho Hình 7.
a) Xác định số đo các góc lượng giác (Oa,Ob), (Ob,Oc) và (Oa,Oc).
b) Nhận xét về mối liên hệ giữa ba số đo góc này.
Trong Hình 15, mâm bánh xe ô tô được chia thành năm phần bằng nhau. Viết công thức số đo tổng quát của góc lượng giác (Ox; ON).
Trên đường tròn lượng giác, hãy biểu diễn các góc lượng giác có số đo có dạng:
a) \(\frac{\pi }{4} + k\pi \,\,\left( {k \in Z} \right)\)
b) \(k\frac{\pi }{4}\,\,\left( {k \in Z} \right)\)
Viết công thức số đo tổng quát của các góc lượng giác (OA; OM) và \(\left( {OA;ON} \right)\) trong Hình 14:
