Sử dụng máy tính cầm tay, tính (kết quả làm tròn đến chữ số thập phân thứ ba):
a) \(\sqrt[3]{79}\); b) \(\sqrt[3]{-6,32}\); c) \(\dfrac{\sqrt[3]{19}+\sqrt[3]{20}}{2}\);
Những câu hỏi liên quan
Sử dụng máy tính cầm tay làm tròn các số sau đến chữ số thập phân thứ nhất:
\(a = \sqrt 2 ;b = \sqrt 5 \)
Tính tổng hai số thập phân nhận được.
Ta có: a = 1,414…; b = 2,236
Làm tròn đến chữ số thập phân thứ nhất, ta được: \(a \approx 1,4;b \approx 2,2\)
Tổng 2 số thập phân nhận được là: 1,4 + 2,2 = 3,6
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
18 tháng 8 2023 lúc 18:07
Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn kết quả đến chữ số thập phân thứ sáu):
a) \({\log _5}0,5\);
b) \(\log 25\);
c) \(\ln \frac{3}{2}\).
a) \(log_50,5=-0,439677\)
c) \(In\left(\dfrac{3}{2}\right)=0,405465\)
Đúng 1
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
18 tháng 8 2023 lúc 18:14
Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn kết quả đến chữ số thập phân thứ tư):
a) \({\log _3}15\);
b) \(\log 8 - \log 3\);
c) \(3\ln 2\).
a) \(log_315=2,4650\)
c) \(3In2=2,0794\)
Đúng 2
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
18 tháng 8 2023 lúc 17:58
a) Sử dụng máy tính cầm tay, hoàn thành bảng sau vào vở (làm tròn kết quả đến chữ số thập phân thứ năm).
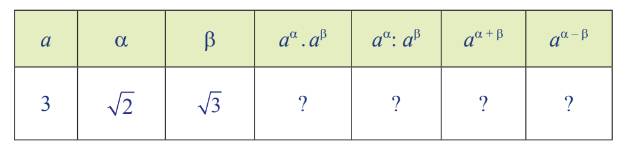
b) Từ kết quả quả ở câu a, có dự đoán gì về tính chất của phép tính luỹ thừa với số mũ thực?
a)
| a | α | b | \(a^{\alpha}\cdot a^{\beta}\) | \(a^{\alpha}:a^{\beta}\) | \(a^{\alpha+\beta}\) | \(\alpha^{\alpha+\beta}\) |
| 3 | \(\sqrt{2}\) | \(\sqrt{3}\) | \(3^{\sqrt{2}}\cdot3^{\sqrt{3}}=31,70659\) | \(3^{\sqrt{2}}:3^{\sqrt{3}}=0,70527\) | \(3^{\sqrt{2}+\sqrt{3}}=31,70659\) | \(3^{\sqrt{2}-\sqrt{3}}=0,70527\) |
b) Nhận xét:
\(a^m\cdot a^n=a^{m+n};a^m:a^n=a^{m-n}\)
Đúng 1
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
18 tháng 8 2023 lúc 17:57
Sử dụng máy tính cầm tay, tính các luỹ thừa sau đây (làm tròn đến chữ số thập phân thứ sáu):
a) \(1,{2^{1,5}}\);
b) \({10^{\sqrt 3 }}\);
c) \({\left( {0,5} \right)^{ - \frac{2}{3}}}\).
a) \(1,2^{1,5}=1,314534\)
b) \(10^{\sqrt{3}}=53,957374\)
c) \(\left(0,5\right)^{-\dfrac{2}{3}}=1,587401\)
Đúng 2
Bình luận (0)
Sử dụng máy tính cầm tay, tính \(\sqrt[3]{{15}}:5 - 2\) (trong kết quả lấy hai chữ số ở phần thập phân).
Bằng máy tính cầm tay, ta tính được kết quả là: \(\sqrt[3]{{15}}:5 - 2 \approx - 1,51\)
Đúng 0
Bình luận (0)
Sử dụng máy tính cầm tay, tìm tập các giá trị x thoả mãn:x^2=8 Làm tròn đến chữ số thập phân thứ 2 Giúp mình với nè mọi người ơi
\(\left[{}\begin{matrix}x=2\sqrt{2}\simeq2.82\\x=-2\sqrt{2}\simeq-2.82\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Sử dụng máy tính cầm tay, tìm tập các giá trị x thỏa mãn: x^2=2.
(làm tròn đến chữ số thập phân thứ hai)
Đáp số:
(các số viết cách nhau bởi dấu ; )
Dùng máy tính cầm tay để tính các căn bậc hai số học sau (làm tròn đến 3 chữ số thập phân).
\(a)\sqrt {2250} ;\,\,\,\,\,\,b)\sqrt {12} ;\,\,\,\,\,\,\,c)\sqrt 5 \,\,\,\,\,\,\,\,\,d)\sqrt {624} \)
\(a)\sqrt {2250} \approx 47,434;\,\,\,\,\,\,b)\sqrt {12} \approx 3,461;\,\,\,\,\,\,\,c)\sqrt 5 \approx 2,236\,\,\,\,\,\,\,\,\,d)\sqrt {624} \approx 24,980\)
Đúng 0
Bình luận (0)
Sử dụng máy tính cầm tay tính các căn bậc hai số học sau (làm tròn kết quả với độ chính xác 0,005, nếu cần).
\(a)\sqrt {15} ;b)\sqrt {2,56} ;c)\sqrt {17256} ;d)\sqrt {793881} \)
Độ chính xác 0,005 tức là ta cần làm tròn đến hàng phần trăm
\(a)\sqrt {15}=3,8729...\approx 3,87\\b)\sqrt {2,56} = 1,6\\c)\sqrt {17256} =131,3620... \approx 131,36\\d)\sqrt {793881} = 891\)
Đúng 0
Bình luận (0)