Chọn ngẫu nhiên một gia đình có hai con và quan sát giới tính của hai người con đó.
a) Phép thử và kết quả của phép thử là gì?
b) Mô tả không gian mẫu của phép thử.
Những câu hỏi liên quan
Gieo đồng thời 1 đồng xu và 1 con xúc xắc. Hãy mô tả không gian mẫu của phép thử và tính xác suất của biến cố A : "Đồng xu xuất hiện mặt sấp và số chấm của con xúc xắc là số chia hết cho 2"
Không gian mẫu \(\Omega=\left\{S;N;1;2;3;4;5;6\right\}\)
\(\Rightarrow n\left(\Omega\right)=8\)
\(A=\left\{S;2;4;6\right\}\)
\(\Rightarrow n\left(A\right)=4\)
Xác suất của biến cố \(A\) :
\(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{4}{8}=\dfrac{1}{2}\)
Đúng 2
Bình luận (0)
Trong một cuộc tổng điều tra dân số, điều tra viên chọn ngẫu nhiên một gia đình có ba người con và quan tâm giới tính của ba người con này.
a) Vẽ sơ đồ hình cây để mô tả các phần tử của không gian mẫu.
b) Giả thiết rằng khả năng sinh con trai và khả năng sinh con gái là như nhau. Tính xác suất để gia đình đó có một con trai và hai con gái.
a, Sơ đồ tư duy:
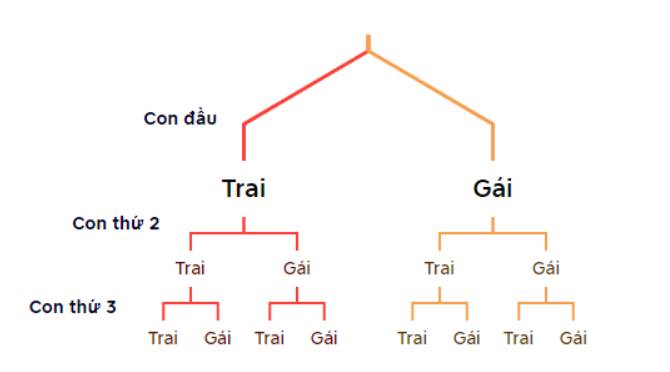
Kí hiệu con trai: T, con gái: G.
Các kết quả có thể xảy ra là: GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT.
Do đó: \(\Omega\)= {GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT}.
Vậy n(Ω) = 8.
b) Gọi biến cố A: “Gia đình đó có một con trai và hai con gái”.
Ta có: A = {GTG; TGG; GGT}. Do đó, \(n(A)\)= 3.
Vậy \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{3}{8}\)
Đúng 0
Bình luận (0)
Xét phép thử T: “Tung một đồng xu hai lần liên tiếp”. Không gian mẫu của phép thử trên là tập hợp Omega {rm{ }} {rm{ }}left{ {SS;{rm{ }}SN;{rm{ }}NS;{rm{ }}NN} right}.a) Sự kiện “Kết quả của hai lần tung là giống nhau” tương ứng với tập con A nào của tập hợp Omega ? b) Phát biểu tập con B{rm{ }} {rm{ }}left{ {SN;{rm{ }}NS} right} của không gian mẫu Omega dưới dạng mệnh đề nêu sự kiện.
Đọc tiếp
Xét phép thử T: “Tung một đồng xu hai lần liên tiếp”. Không gian mẫu của phép thử trên là tập hợp \(\Omega {\rm{ }} = {\rm{ }}\left\{ {SS;{\rm{ }}SN;{\rm{ }}NS;{\rm{ }}NN} \right\}.\)
a) Sự kiện “Kết quả của hai lần tung là giống nhau” tương ứng với tập con A nào của tập hợp \(\Omega \)?
b) Phát biểu tập con \(B{\rm{ }} = {\rm{ }}\left\{ {SN;{\rm{ }}NS} \right\}\) của không gian mẫu \(\Omega \) dưới dạng mệnh đề nêu sự kiện.
a) Sự kiện “Kết quả của hai lần tung là giống nhau” tương ứng với tập con \(A{\rm{ }} = {\rm{ }}\left\{ {SS;{\rm{ }}NN} \right\}\)
b) Tập con \(B{\rm{ }} = {\rm{ }}\left\{ {SN;{\rm{ }}NS} \right\}\) của không gian mẫu \(\Omega \) được phát biểu dưới dạng mệnh đề nêu sự kiện là: “Kết quả của hai lần tung là khác nhau”.
Đúng 0
Bình luận (0)
Xét phép thử gieo một con xúc xắc cân đối, đồng chất hai lần. Số phần tử của không gian mẫu là
A. 10
B. 12
C. 8
D. 36
Đáp án D
Số phần tử của không gian mẫu là Ω = C 6 1 . C 6 1 = 6.6 = 36
Đúng 0
Bình luận (0)
Xét phép thử gieo một con xúc xắc cân đối, đồng chất hai lần. Số phần tử của không gian mẫu là
A. 10
B. 12
C. 8
D. 36
Đáp án D
Số phần tử của không gian mẫu là Ω = C 6 1 . C 6 1 = 6 . 6 = 36 .
Đúng 0
Bình luận (0)
Lấy ngẫu nhiên một quả bóng từ hộp ở ví dụ 2, xem số, sau đó trả lại hộp, trộn đều rồi lại lấy ngẫu nhiên một quả bóng từ hộp đó. Hãy xác định không gian mẫu của phép thử hai lần lấy bóng này.
Do lần đầu tiên lấy bóng sau đó trả lại hộp nên lần hai có thể lấy 1 trong 4 quả bóng và hai lần lấy lần lượt nên ta cần phải tính đến thứ tự lấy bóng. Nếu lần đầu lấy được bóng 1 và lần hai lấy được bóng 3 thì ta sẽ kí hiệu kết quả của phép thử là cặp (1; 3). Khi đó không gian mẫu của phép thử là:
\(\Omega = \left\{ \begin{array}{l}(1;1);(1;2);(1;3);(1;4);(2;1);(2;2);(2;3);(2;4);\\(3;1);(3;2);(3;3);(3;4);(4;1);(4;2);(4;3);(4;4)\end{array} \right\}\)
Đúng 0
Bình luận (0)
Xét một phép thử có không gian mẫu
Ω
và A là một biến cố của phép thử đó. Phát biểu nào dưới đây là sai? A. P(A) 0 khi và chỉ khi A là chắc chắn B.
0
≤
P
A
≤
1
C. Xác suất của biến cố A là số
P
A
n
A
n
Ω...
Đọc tiếp
Xét một phép thử có không gian mẫu Ω và A là một biến cố của phép thử đó. Phát biểu nào dưới đây là sai?
A. P(A) = 0 khi và chỉ khi A là chắc chắn
B. 0 ≤ P A ≤ 1
C. Xác suất của biến cố A là số P A = n A n Ω
D. P A = 1 - P A
Đáp án A
Các phát biểu B, C và D là đúng; phát biểu A là sai
Đúng 0
Bình luận (0)
Xét một phép thử có không gian mẫu
Ω
và
A
là một biến cố của phép thử đó. Phát biểu nào dưới đây là sai? A. P(A) 0 khi và chỉ khi A là chắc chắn B.
0
≤
P
(
A
)
≤
1
C. Xác suất của biến cố
A
là số ...
Đọc tiếp
Xét một phép thử có không gian mẫu Ω và A là một biến cố của phép thử đó. Phát biểu nào dưới đây là sai?
A. P(A) = 0 khi và chỉ khi A là chắc chắn
B. 0 ≤ P ( A ) ≤ 1
C. Xác suất của biến cố A là số P ( A ) = n ( A ) n ( Ω )
D. P ( A ) = 1 - P ( A ¯ )
Đáp án A
Các phát biểu B, C và D là đúng; phát biểu A là sai
Đúng 0
Bình luận (0)
Xét một phép thử có không gian mẫu
Ω
và A là một biến cố của phép thử đó. Phát biểu nào sau đây sai? A. Xác suất của biến cố A là
P
A
n
A
n
Ω
.
B.
0
≤
P
A
≤
1
.
C. ...
Đọc tiếp
Xét một phép thử có không gian mẫu Ω và A là một biến cố của phép thử đó. Phát biểu nào sau đây sai?
A. Xác suất của biến cố A là P A = n A n Ω .
B. 0 ≤ P A ≤ 1 .
C. P A = 1 - P A ¯ .
D. P A = 0 khi và chỉ khi A là biến cố chắc chắn.
Xét một phép thử có không gian mẫu
Ω
và A là một biến cố của phép thử đó. Phát biểu nào sau đây sai ? A. Xác suất của biến cố A là P(A)
n
(
A
)
n
(
Ω
)
B. 0
≤
P(A)1 C. P(A) 1 -
P
(
A
¯...
Đọc tiếp
Xét một phép thử có không gian mẫu Ω và A là một biến cố của phép thử đó. Phát biểu nào sau đây sai ?
A. Xác suất của biến cố A là P(A) = n ( A ) n ( Ω )
B. 0 ≤ P(A)1
C. P(A) = 1 - P ( A ¯ ) .
D. P(A) = 0 khi và chỉ khi A là biến cố chắc chắn.
Chọn D
Theo định nghĩa biến cố chắc chắn ta có: Với A là biến cố chắc chắn thì n(A) = n( Ω )
Suy ra: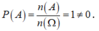 
.
Đúng 0
Bình luận (0)