Chứng minh rằng nếu một điểm thuộc đường tròn (O) thì:
a) Điểm đối xứng với nó qua tâm O cũng thuộc (O).
b) Điểm đối xứng với nó qua một đường thẳng d tùy ý đi qua O cũng thuộc (O).
Cho đường tròn (O), A là một điểm bất kì thuộc đường tròn. Vẽ A’ đối xứng với A qua O (h.56). Chứng minh rằng điểm A’ cũng thuộc đường tròn (O).
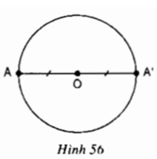
Do A' đối xứng với A qua O nên O là trung điểm của AA' ⇒ OA = OA' = R
⇒ A' cũng thuộc đường tròn (O)
Cho đường tròn (O), A là một điểm bất kì thuộc đường tròn. Vẽ A’ đối xứng với A qua O (h.56). Chứng minh rằng điểm A’ cũng thuộc đường tròn (O).
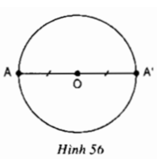
Do A' đối xứng với A qua O nên O là trung điểm của AA' ⇒ OA = OA' = R
⇒ A' cũng thuộc đường tròn (O)
Cho đường tròn (O), AB là một đường kính bất kì và C là một điểm thuộc đường tròn. Vẽ C’ đối xứng với điểm C qua AB (h.57). Chứng minh rằng điểm C’ cũng thuộc đường tròn (O).
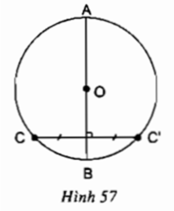
Do C và C' đối xứng nhau qua AB nên AB là đường trung trực của CC'
⇒ O nằm trên đường trung trực của CC'
⇒ OC = OC' = R
⇒ C' cũng thuộc đường tròn (O)
Cho đường tròn (O), AB là một đường kính bất kì và C là một điểm thuộc đường tròn. Vẽ C’ đối xứng với điểm C qua AB (h.57). Chứng minh rằng điểm C’ cũng thuộc đường tròn (O).
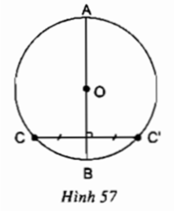
Do C và C' đối xứng nhau qua AB nên AB là đường trung trực của CC'
⇒ O nằm trên đường trung trực của CC'
⇒ OC = OC' = R
⇒ C' cũng thuộc đường tròn (O)
a). Cho đường trong tâm O, A là điểm bất kì thuộc đường tròn. Vẽ A' đối xứng với A qua O. Chứng minh rằng điểm A' cũng thuộc đường tròn tâm O.
b). Cho đường tròn (O), AB là một đường kính bất kì và C là điểm thuộc đường tròn. Vẽ C' đối xứng với C qua AB. Chứng minh rằng điểm C' cũng thuộc đường tròn (O).
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O.
Gọi M là một điểm trên cung nhỏ B C ⏜ (M khác B; C và AM không đi qua O).
Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.
1). Gọi D là điểm đối xứng với điểm M qua O. Chứng minh rằng ba điểm N, P, D thẳng hàng.
2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.
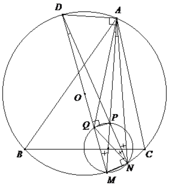
1). Vì MP là đường kính suy ra P N ⊥ M N (1).
Vì MD là đường kính suy ra D N ⊥ M N (2).
Từ (1) và (2), suy ra N; P; D thẳng hàng.
Cho đường tròn (O), đường kính AB, điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao điểm của AC và Bm. Gọi F là điểm đối xứng với E qua M. Chứng minh rằng FA là tiếp tuyến của đường tròn (O)
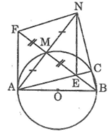
Ta có: MA = MN (tính chất đối xứng tâm)
ME = MF (tính chất đối xứng tâm)
Tứ giác AENF có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành
Suy ra: AF // NE
Mà NE ⊥ AB (chứng minh trên)
Suy ra: AF ⊥ AB tại A
Vậy FA là tiếp tuyến của đường tròn (O).
Giải bài :Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN với M thuộc (O) và N thuộc (O'). Gọi P là điểm đối xứng với M qua OO', Q là điểm đối xứng với N qua OO'. Chứng minh rằng: a/ MNPQ là hình thang cân.
Cho tam giác OAB vuông tại A (OA<BA). Lấy điểm C đối xứng với A qua OB.
a) chứng minh rằng 4 điểm o,a,b,c cùng thuộc một đường tròn
b) đường tròn tâm O đường kính CD cắt BD tại E. Chứng minh AD//OB
Vẽ hình giúp em với ạ.
Cho đường tròn (O; R) đường kính AB, lấy điểm M thuộc (O) sao cho góc MAB = 30°. Gọi C là điểm đối xứng với điểm O qua điểm B. Qua điểm C, vẽ đường thẳng vuông góc với AB cắt đường thăng AM tại D. a) Chứng minh: tứ giác BCDM nội tiếp trong đường tròn tâm I. Xác định vị trí điểm I b) Chứng minh: AD.AM = 6R² c) Tính số đo của góc ADC
a: góc AMB=1/2*sđ cung AB=90 độ
góc BMD+góc BCD=180 độ
=>BMDC nội tiếp
b: Xét ΔAMB vuông tại M và ΔACD vuông tại C có
góc MAB chung
=>ΔAMB đồng dạng với ΔACD
=>AM/AC=AB/AD
=>AM*AD=AB*AC=6R^2
c: góc ADC=90-30=60 độ