Do A' đối xứng với A qua O nên O là trung điểm của AA' ⇒ OA = OA' = R
⇒ A' cũng thuộc đường tròn (O)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
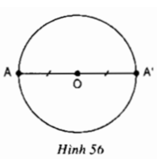
Cho đường tròn (O), A là một điểm bất kì thuộc đường tròn. Vẽ A’ đối xứng với A qua O (h.56). Chứng minh rằng điểm A’ cũng thuộc đường tròn (O).
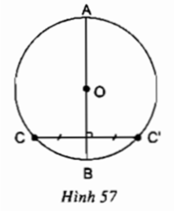
Cho đường tròn (O), AB là một đường kính bất kì và C là một điểm thuộc đường tròn. Vẽ C’ đối xứng với điểm C qua AB (h.57). Chứng minh rằng điểm C’ cũng thuộc đường tròn (O).
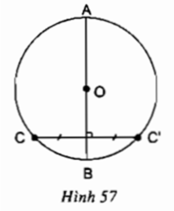
Cho đường tròn (O), AB là một đường kính bất kì và C là một điểm thuộc đường tròn. Vẽ C’ đối xứng với điểm C qua AB (h.57). Chứng minh rằng điểm C’ cũng thuộc đường tròn (O).
Cho đường tròn (O), đường kính AB, điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao điểm của AC và Bm. Gọi F là điểm đối xứng với E qua M. Chứng minh rằng FA là tiếp tuyến của đường tròn (O)
Cho đường tròn (O) bán kính OA = R Vẽ dây BC vuông góc với OA tại trung điểm H của OA.
a) Tứ giác ABOC là hình gì? Vì sao?
b) Gọi K là điểm đối xứng với O qua A Chứng minh rằng K, B, O, C cùng thuộc một đường tròn
Cho đường tròn (O), đường kính AB, điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao điểm của AC và Bm. Chứng minh rằng NE ⊥ AB
Cho đường tròn (O;R) đường kính AB, điểm C thuộc đường tròn (O) sao cho CA < CB. Vẽ dây CD vuông góc với AB tại H. Gọi E là điểm điểm đối xứng với A qua H.
Chứng minh ACED là hình thoi
Cho đường tròn (O), đường kính AB, điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao điểm của AC và Bm. Chứng minh rằng FN là tiếp tuyến của đường tròn (B; BA)
7 tháng 1 2022 lúc 6:46
Cho đường tròn (O), đường kính AB, điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao điểm của AC và BM. Gọi F là điểm đối xứng với E qua M
d, chứng minh BM.BF=BF2-FN2