Xét tam giác đều ABC có cạnh bằng 2a.
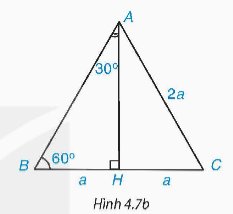
a) Tính đường cao AH của tam giác ABC (H.4.7b).
b) Tính sin30°, cos30°, sin60° và cos60°.
c) Tính tan30°, cot30°, tan60° và cot60°.
Cho tam giác ABC đều cạnh a, kẻ đường cao AH. Tính tỉ số lượng giác của HAC. Tính tỉ số lượng giác của góc C. Suy ra sin30°, cos30°, tg30 cotg30°, sin60°, cos60°, tg60°, cotg60
ΔABC đều có AH là đường cao
nên AH=a*căn 3/2; H là trung điểm của BC
=>HB=HC=a/2
sin HAC=cos C=HC/AC=1/2
=>sin30=cos60=1/2
cos HAC=sin C=AH/AC=căn 3/2
=>cos30=sin60=căn 3/2
tan HAC=cot C=HC/AH=1/căn 3
=>tan 30=cot 60=1/căn 3
cot HAC=tan C=1:1/căn 3=căn 3
=>cot 30=tan 60=căn 3
Tính giá trị biểu thức P = cos 30 ∘ cos 60 ∘ − sin 30 ∘ sin 60 ∘ .
A. P = 3 .
B. P = 3 2 .
C. P=1
D. P = 0
Vì 300 và 600 là hai góc phụ nhau nên sin 30 0 = cos 60 0 sin 60 0 = cos 30 0
⇒ P = cos 30 ∘ cos 60 ∘ − sin 30 ∘ sin 60 ∘ = cos 30 ∘ cos 60 ∘ − cos 60 ∘ cos 30 ∘ = 0.
Chọn D.
Tính giá trị biểu thức P = sin 30 ∘ cos 60 ∘ + sin 60 ∘ cos 30 ∘ .
A. P = 1
B. P = 0
C. P = 3 .
D. P = - 3 .
Vì 300 và 600 là hai góc phụ nhau nên sin 30 0 = cos 60 0 sin 60 0 = cos 30 0
⇒ P = sin 30 ∘ cos 60 ∘ + sin 60 ∘ cos 30 ∘ = cos 2 60 ∘ + sin 2 60 ∘ = 1.
Chọn A.
Tính giá trị biểu thức P = cos 30 ∘ cos 60 ∘ − sin 30 ∘ sin 60 ∘
A. P = 3 .
B. P = 3 2 .
C. P = 1
D. P= 0
Vì 300 và 600 là hai góc phụ nhau nên sin 30 0 = cos 60 0 sin 60 0 = cos 30 0
⇒ P = cos 30 ∘ cos 60 ∘ − sin 30 ∘ sin 60 ∘ = cos 30 ∘ cos 60 ∘ − cos 60 ∘ cos 30 ∘ = 0.
Chọn D.
Cho tan giác đều cạnh a, kẻ AH vuông góc với BC. Tính tỉ số lượng giác của góc HAC, góc C. Suy ra Sin30°, Cos30°, Tan30°, Cot30°
Cho tam giác ABC cân tại A, đường cao AH (H thuộc BC )a, tam giác ABH bằng tam giác ACH. B, lấy K là trung điểm của AC gọi g là giao điểm của AH và BK điểm g có cách đều ba cạnh của tam giác ABC không? vì sao? c, AC = 2 cm tính AH=? (Hãy nêu giả thiết và kết luận và vẽ hình)
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: G ko cách đều ba cạnh của ΔABC vì G ko phải là tâm đường tròn nội tiếp tam giác
Cho tam giác đều ABC có cạnh bằng a và đường cao AH. Tính diện tích xung quanh của hình nón tạo thành khi quay tam giác ABC quanh trục AH.
A. 2 π a 2
B. π a 2
C. 3 4 π a 2
D. 1 2 π a 2
Bán kính đáy:

Diện tích xung quanh của hình nón đó là:
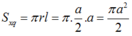
Chọn: D
Cho tam giác đều ABC có cạnh bằng a và đường cao AH. Tính diện tích xung quanh của hình nón tạo thành khi quay tam giác ABC quanh trục AH.
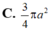
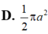
Cho tam giác đều ABC có cạnh bằng a và đường cao AH. tính AH
Do `\Delta ABC` đều
`-> AB=AC=BC`
`-> AB = 2BH`
Xét `\Delta ABH` vuông tại `H` `( AH` là đường cao `)`
ta có `:` `AB^2 = BH^2 + AH^2`
`=> 4BH^2 = BH^2 + AH^2`
`=> 3BH^2 = AH^2`
`=> BH = ( AH )/( \sqrt{3} )`
`=> a = AB = ( AH )/( \sqrt{3} )`
Vậy `...`
`=> a = AB = ( AH )/( \sqrt{3} )`
dòng cuối
`=> a = AB = ( 2AH )/( \sqrt{3} )`
dòng cuối
4. a)Tính cạnh góc vuông của một tam giác vuông cân có cạnh huyền bằng a.
b) Tính cạnh của một tam giác đều có đường cao bằng h.
5. Cho tam giác nhọn ABC, đường cao AH = 12 cm, AB = 13 cm, HC = 16 cm. Tính các độ dài AC, BC.
4:
a: Gọi độ dài cạnh góc vuông cần tìm là x
Theo đề, ta có: x^2+x^2=a^2
=>2x^2=a^2
=>x^2=a^2/2=2a^2/4
=>\(x=\dfrac{a\sqrt{2}}{2}\)
b:
Độ dài cạnh là;
\(h:\dfrac{\sqrt{3}}{2}=\dfrac{2h}{\sqrt{3}}\)
5:
ΔAHB vuông tại H
=>AH^2+HB^2=AB^2
=>13^2=12^2+HB^2
=>HB=5cm
BC=5+16=21cm
ΔAHC vuông tại H
=>AH^2+HC^2=AC^2
=>AC^2=16^2+12^2=400
=>AC=20(cm)