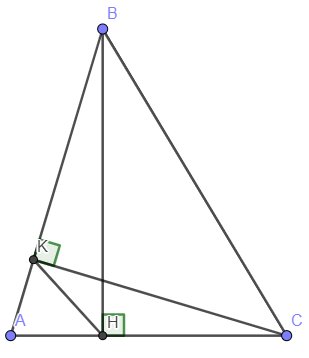
Cho tam giác nhọn ABC có đường cao CK. Biểu diễn CK theo AC và sinA. Từ đó, chứng minh diện tích của tam giác ABC bằng \(\dfrac{1}{2}\).AB.AC.sinA.

Những câu hỏi liên quan
Cho tam giác ABC có hai đường cao BH và CK. Chứng minh rằng: Tỉ số diện tích của tam giác AHK với tam giác ABC bằng cos^2 A
Mọi người giúp mình với ![]()
Ai giỏi toán làm hộ mình với
Cho tam giác nhọn ( AB<AC) có các đường cao BH và CK cắt nhau tại F
a) Chứng minh tam giác ABC ᔕ tam giác ACK
b) Chứng minh \(\dfrac{EK}{EB}=\dfrac{EH}{EC}\)
c) So sánh góc AKH và góc ACB
d) Chứng minh BE.BH+CE.CK=BC\(^2\)
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
\(\widehat{BAH}\) chung
Do đó: ΔABH\(\sim\)ΔACK
b: Xét ΔKEB vuông tại K và ΔHEC vuông tại H có
\(\widehat{KEB}=\widehat{HEC}\)
DO đó: ΔKEB\(\sim\)ΔHEC
Suy ra: EK/EH=EB/EC
hay \(\dfrac{EK}{EB}=\dfrac{EH}{EC}\)
c: Xét ΔAKH và ΔACB có
AK/AC=AH/AB
góc A chung
Do đó: ΔAKH\(\sim\)ΔACB
Suy ra: \(\widehat{AKH}=\widehat{ACB}\)
Đúng 1
Bình luận (1)
Cho tam giác abc cân tại a gọi bh,ck lần lượt là đường cao xuất phát từ điểm b và c của tam giác abc. Chứng minh bh= ck. Dựa theo công thưc tính diện tích hình tam giác . Gap lắm rùi cac bạn giúp vs nha
Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
góc BAH chung
Do đó: ΔABH=ΔACK
Suy ra: BH=CK
Đúng 0
Bình luận (0)
1. Cho tam giác ABC có diện tích bằng 24cm2, đường cao AH bằng 6 cm. Tính BC
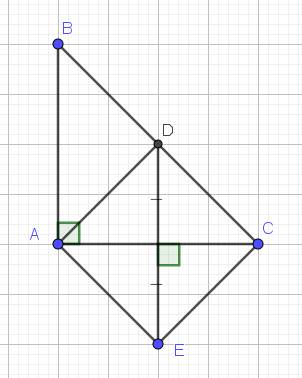
2. Cho tam giác ABC vuông cân tại A (AD là phân giác CD thuộc BC), E là điểm đối xứng với D qua AC. Tứ giác AECD là hình gì?
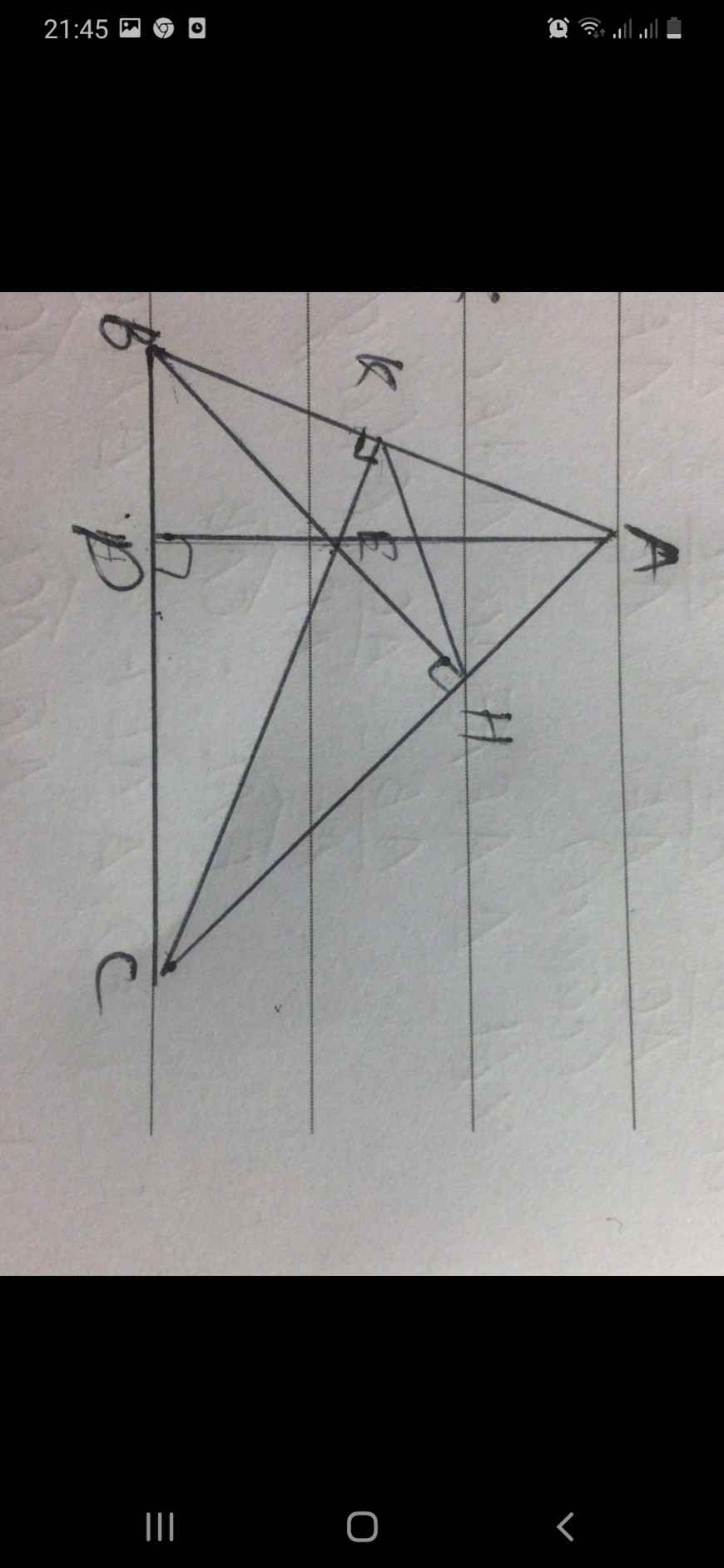
3. Cho tam giác nhọn ABC, các đường cao BH và CK. Gọi E và F lần lượt là hình chiếu của B và C trên HK. Chứng minh rằng EK = HF
Bài 2:
Tam giác $ABC$ cân tại $A$ nên phân giác $AD$ đồng thời là đường cao
$\Rightarrow AD\perp DC$. Mà $\widehat{DAC}=\widehat{BAC}:2 =45^0$ nên $\triangle DAC$ vuông cân tại $D$
$\Rightarrow DA=DC(1)$
$D,E$ đối xứng với nhau qua $AC$ nên $AC$ là trung trực của $DE$
$\Rightarrow CD=CE; AD=AE(2)$
Từ $(1); (2)\Rightarrow AD=DC=CE=EA$
$\Rightarrow ADCE$ là hình thoi.
Mà $\widehat{ADC}=90^0$ nên $ADCE$ là hình vuông.
Đúng 1
Bình luận (0)
Bài 3:
Xét tam giác $ABH$ và $ACK$ có:
$\widehat{AHB}=\widehat{AKC}=90^0$
$\widehat{A}$ chung
$\Rightarrow \triangle ABH\sim \triangle ACK$ (g.g)
$\Rightarrow \frac{AB}{AH}=\frac{AC}{AK}$
Xét tam giác $AKH$ và $ACB$ có:
$\widehat{A}$ chung
$\frac{AH}{AB}=\frac{AK}{AC}$ (cmt)
$\Rightarrow \triangle AKH\sim \triangle ACB$ (c.g.c)
$\Rightarrow \widehat{K_2}=\widehat{ACB}$ và $\widehat{H_1}=\widehat{ABC}$
Xét tam giác $KEB$ và $CHB$ có:
$\widehat{KEB}=\widehat{CHB}=90^0$
$\widehat{K_1}=\widehat{K_2}=\widehat{ACB}=\widehat{HCB}$ (cmt)
$\Rightarrow \triangle KEB\sim \triangle CHB$ (g.g)
$\Rightarrow \frac{KE}{KB}=\frac{CH}{CB}(1)$
Tương tự:
$\triangle CFH\sim \triangle CKB$ (c.g.c)
$\Rightarrow \frac{CH}{FH}=\frac{CB}{KB}(2)$
Từ $(1); (2)\Rightarrow \frac{KE}{KB}.\frac{CH}{FH}=\frac{CH}{CB}.\frac{CB}{KB}$
$\Rightarrow \frac{KE}{HF}=1$
$\Rightarrow KE=HF$ (đpcm)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Ai giỏi toán làm hộ mình với
Cho tam giác nhọn ( AB<AC) có các đường cao BH và CK cắt nhau tại F
a) Chứng minh tam giác ABC ᔕ tam giác ACK
b) Chứng minh \(\dfrac{EK}{EB}=\dfrac{EH}{EC}\)
c) So sánh góc AKH và góc ACB
d) Chứng minh BE.BH+CE.CK=BC2
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
\(\widehat{BAH}\) chung
Do đó: ΔABH\(\sim\)ΔACK
b: Xét ΔKEB vuông tại K và ΔHEC vuông tại H có
\(\widehat{KEB}=\widehat{HEC}\)
DO đó: ΔKEB\(\sim\)ΔHEC
Suy ra: EK/EH=EB/EC
hay \(\dfrac{EK}{EB}=\dfrac{EH}{EC}\)
c: Xét ΔAKH và ΔACB có
AK/AC=AH/AB
góc A chung
Do đó: ΔAKH\(\sim\)ΔACB
Suy ra: \(\widehat{AKH}=\widehat{ACB}\)
Đúng 1
Bình luận (1)
Ai giỏi toán làm hộ mình với
Cho tam giác nhọn ( AB<AC) có các đường cao BH và CK cắt nhau tại F
a) Chứng minh tam giác ABC ᔕ tam giác ACK
b) Chứng minh \(\dfrac{EK}{EB}=\dfrac{EH}{EC}\)
c) So sánh góc AKH và góc ACB
d) Chứng minh BE.BH+CE.CK=BC2
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O,R), (AB<AC). Ba đường cao AE,BF,CK của tam giác ABC cắt nhau tại H. Vẽ đường kính AD của đường tròn (O,R)
a) Chứng minh: Tứ giác AKHF nội tiếp
b) Chứng minh DC//BF
c) Chứng minh: AB.AC=AE.AD
d) Cho BC=\(\frac{4\sqrt{2}R}{3}\). Tính theo R diện tích hình tròn ngoại tiếp tam giác HKF
Cho tam giác ABC có 3 góc nhọn. Các đường cao BI và CK cắt nhau tại Ha) chứng minh: tam giác ABI đồng dạng tam giác ACKb) chứng minh HK nhân HC=HB nhân HIc) cho AB=6cm, AC=8cm, CI=5cm. Tính độ dài đoạn thẳng CK
a) Xét ΔABI vuông tại I và ΔACK vuông tại K có
\(\widehat{BAI}\) chung
Do đó: ΔABI\(\sim\)ΔACK(g-g)
Đúng 0
Bình luận (0)
cho tam giác ABC biết AB=AC. Kẻ đường cao BH và CK.
a) Viết công thức tính diện tích tam giác ABC theo độ dài đường cao BH VÀ CK.
b)tỉ số 2 đường chép xuất phát từ các đỉnh B cà C.
c)so sánh độ dài 2 đường cao BH VÀ CK.
Cho tam giác nhọn ABC có AB>ACm đường cao AD. Trên đoạn DC lấy điểm E sao cho DB=DE. a) Chứng minh tam giác ABE cân b) Từ E kẻ EF vuông góc với AC(F thuộc AC). Từ C kẻ CK vuông góc với AE(K thuộc AE). Chứng minh ba đường thẳng AD, EF và CK đồng quy.
a: Xét ΔABE có
AD vừa là đường cao, vừa là trung tuyến
=>ΔABE cân tại A
b: Gọi M là giao của AD và FE
Xét ΔAME có
ED,AF là đường cao
ED cắt AF tại C
=>C là trực tâm
=>M,C,K thẳng hàng
=>ĐPCM
Đúng 1
Bình luận (0)