Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y=2\sqrt{1-x^2}+x^2\).

Những câu hỏi liên quan
Gọi M,m lần lượt là giá trị lớn nhất , giá trị nhỏ nhất của hàm số y=\(\sqrt{1+x}+\sqrt{1-x}\). Giá trị của M+m là
A.4 B.2+\(\sqrt{2}\) C.4+\(\sqrt{2}\) D.2
Gọi M,m lần lượt là giá trị lớn nhất , giá trị nhỏ nhất của hàm số y=\(\sqrt{1+x}+\sqrt{1-x}\). Giá trị của M+m là
A.4 B.2+\(\sqrt{2}\) C.4+\(\sqrt{2}\) D.2
Giải thích hộ em với
tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số \(y=\frac{x+1}{\sqrt{x^2+1}}\) trên [-1;2]
Tìm giá trị lớn nhất, giá trị lớn nhất của hàm số (nếu có)
a, \(y=\sqrt{x^2+x-2}\)
b, \(y=\sqrt{2+x}+\sqrt{4-x}\)
c, \(y=x+\sqrt{4-x^2}\)
Lời giải:
a. $y=\sqrt{x^2+x-2}\geq 0$ (tính chất cbh số học)
Vậy $y_{\min}=0$. Giá trị này đạt tại $x^2+x-2=0\Leftrightarrow x=1$ hoặc $x=-2$
b.
$y^2=6+2\sqrt{(2+x)(4-x)}\geq 6$ do $2\sqrt{(2+x)(4-x)}\geq 0$ theo tính chất căn bậc hai số học
$\Rightarrow y\geq \sqrt{6}$ (do $y$ không âm)
Vậy $y_{\min}=\sqrt{6}$ khi $x=-2$ hoặc $x=4$
$y^2=(\sqrt{2+x}+\sqrt{4-x})^2\leq (2+x+4-x)(1+1)=12$ theo BĐT Bunhiacopxky
$\Rightarrow y\leq \sqrt{12}=2\sqrt{3}$
Vậy $y_{\max}=2\sqrt{3}$ khi $2+x=4-x\Leftrightarrow x=1$
c. ĐKXĐ: $-2\leq x\leq 2$
$y^2=(x+\sqrt{4-x^2})^2\leq (x^2+4-x^2)(1+1)$ theo BĐT Bunhiacopxky
$\Leftrightarrow y^2\leq 8$
$\Leftrightarrow y\leq 2\sqrt{2}$
Vậy $y_{\max}=2\sqrt{2}$ khi $x=\sqrt{2}$
Mặt khác:
$x\geq -2$
$\sqrt{4-x^2}\geq 0$
$\Rightarrow y\geq -2$
Vậy $y_{\min}=-2$ khi $x=-2$
Đúng 1
Bình luận (0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
\(y=sin\dfrac{2x}{x^2+1}+cos\dfrac{x}{x^2+1}+1\)
tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số trên đoạn [2;4]
y=\(\dfrac{x^2+3}{x-1}\)
tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau:
\(y=2cos^2x-2\sqrt{3}sinxcosx+1\)
\(y=2cos^2x-2\sqrt{3}sinx.cosx+1\)
\(=2cos^2x-1-2\sqrt{3}sinx.cosx+2\)
\(=cos2x-\sqrt{3}sin2x+2\)
\(=2\left(\dfrac{1}{2}cos2x-\dfrac{\sqrt{3}}{2}sin2x\right)+2\)
\(=2cos\left(2x+\dfrac{\pi}{3}\right)+2\)
Ta có: \(cos\left(2x+\dfrac{\pi}{3}\right)\in\left[-1;1\right]\)
\(\Rightarrow min=0\Leftrightarrow cos\left(2x+\dfrac{\pi}{3}\right)=-1\Leftrightarrow2x+\dfrac{\pi}{3}=\pi+k2\pi\Leftrightarrow x=\dfrac{\pi}{3}+k\pi\)
\(\Rightarrow max=4\Leftrightarrow cos\left(2x+\dfrac{\pi}{3}\right)=1\Leftrightarrow2x+\dfrac{\pi}{3}=k2\pi\Leftrightarrow x=-\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
Đúng 1
Bình luận (0)
\(y=2cos^2x-\sqrt{3}sin2x+1=cos2x-\sqrt{3}sin2x+2\)
\(y=2.cos\left(2x+\dfrac{\pi}{3}\right)+2\)
\(\forall x\in R->-1\le cos\left(2x+\dfrac{\pi}{3}\right)\)
=> \(Min_y=2.\left(-1\right)+2=0\)
Mặt khác, theo Bunhiacopxki:
\(\left(cos2x+\sqrt{3}sin2x\right)^2\le\left(1^2+\sqrt{3}^2\right)\left(cos^22x+sin^22x\right)=4\)
=>\(Max_y=4\)
Đúng 1
Bình luận (0)
Cho hàm số y = \(|2x-x^2-\sqrt{\left(x+1\right)\left(3-x\right)}+b|\)Để giá trị lớn nhất của hàm số đạt giá trị nhỏ nhất thì giá trị của b thuộc khoảng nào
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số :
a. y=\(\sqrt{\text{3(1+ sin(x))}}\)-5
b. y= 6 sin(x+8)-5
Lập bảng biến thiên của hàm số \(y = {x^2} + 2x + 3.\) Hàm số này có giá trị lớn nhất hay giá trị nhỏ nhất? Tìm giá trị đó.
Tham khảo:
Đỉnh S có tọa độ: \({x_S} = \dfrac{{ - b}}{{2a}} = \dfrac{{ - 2}}{{2.1}} = - 1;\,{y_S} = {\left( { - 1} \right)^2} + 2.( - 1) + 3 = 2.\)
Hay \(S\left( { - 1;2} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:
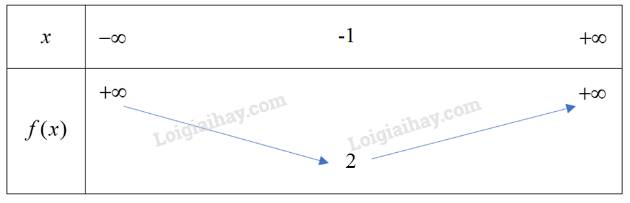
Hàm số đạt giá trị nhỏ nhất bằng \(2\).
Đúng 0
Bình luận (0)






















