MN GIÚP MIK VS Ạ
cả hai bài đều tính theo kiểu trục căn thức ở mẫu rồi tính nha :>>

Trục căn thức ở mẫu : a . 6/5√8 ; b. 7/5+2√3 ; c. 6/√7 - √5 Giúp mik vs ạ
a: \(\dfrac{6}{5\sqrt{8}}=\dfrac{6}{10\sqrt{2}}=\dfrac{3}{5\sqrt{2}}=\dfrac{3\sqrt{2}}{10}\)
b: \(\dfrac{7}{5+2\sqrt{3}}=\dfrac{7\left(5-2\sqrt{3}\right)}{13}\)
c: \(\dfrac{6}{\sqrt{7}-\sqrt{5}}=\dfrac{6\left(\sqrt{7}+\sqrt{5}\right)}{2}=3\left(\sqrt{7}+\sqrt{5}\right)\)
a) \(\dfrac{6}{5\sqrt{8}}\)
\(=\dfrac{6}{5\cdot2\sqrt{2}}\)
\(=\dfrac{6}{10\sqrt{2}}\)
\(=\dfrac{3\sqrt{2}}{5\sqrt{2}\cdot\sqrt{2}}\)
\(=\dfrac{3\sqrt{2}}{10}\)
b) \(\dfrac{7}{5+2\sqrt{3}}\)
\(=\dfrac{7\left(5-2\sqrt{3}\right)}{\left(5+2\sqrt{3}\right)\left(5-2\sqrt{3}\right)}\)
\(=\dfrac{7\left(5-2\sqrt{3}\right)}{5^2-\left(2\sqrt{3}\right)^2}\)
\(=\dfrac{7\left(5-2\sqrt{3}\right)}{13}\)
\(=\dfrac{35-14\sqrt{3}}{13}\)
c) \(\dfrac{6}{\sqrt{7}-\sqrt{5}}\)
\(=\dfrac{6\left(\sqrt{7}+\sqrt{5}\right)}{\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)}\)
\(=\dfrac{6\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=3\sqrt{7}+3\sqrt{5}\)
có ai biết giải bài này k hộ mình vs ( chi tiết hộ mình nhé )
bài 1: trục căn thức ở mẫu và rút gọn
a, \(\dfrac{1}{2\sqrt{2}-3\sqrt{3}}\)
b, \(\sqrt{\dfrac{3-\sqrt{5}}{3+\sqrt{5}}}\)
bài 2: trục căn thức ở mẫu và rút gọn
a, \(\dfrac{\sqrt{8}}{\sqrt{5}-\sqrt{3}}\)
b, \(\sqrt{\dfrac{2-\sqrt{3}}{2+\sqrt{3}}}\)
bài 3: trục căn thức và thực hiện phép tính
a, M=\(\left(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}\right).\left(\sqrt{6}+11\right)\)
b, N= \(\left(1-\dfrac{5+\sqrt{5}}{1+\sqrt{5}}\right).\left(\dfrac{5-\sqrt{5}}{1-\sqrt{5}}-1\right)\)
Bài 1:
a.
\(\frac{1}{2\sqrt{2}-3\sqrt{3}}=\frac{2\sqrt{2}+3\sqrt{3}}{(2\sqrt{2}-3\sqrt{3})(2\sqrt{2}+3\sqrt{3})}=\frac{2\sqrt{2}+3\sqrt{3}}{(2\sqrt{2})^2-(3\sqrt{3})^2}=\frac{2\sqrt{2}+3\sqrt{3}}{-19}\)
b.
\(=\sqrt{\frac{(3-\sqrt{5})^2}{(3-\sqrt{5})(3+\sqrt{5})}}=\sqrt{\frac{(3-\sqrt{5})^2}{3^2-5}}=\sqrt{\frac{(3-\sqrt{5})^2}{4}}=\sqrt{(\frac{3-\sqrt{5}}{2})^2}=|\frac{3-\sqrt{5}}{2}|=\frac{3-\sqrt{5}}{2}\)
Bài 2.
a.
\(=\frac{\sqrt{8}(\sqrt{5}+\sqrt{3})}{(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})}=\frac{2\sqrt{2}(\sqrt{5}+\sqrt{3})}{5-3}=\sqrt{2}(\sqrt{5}+\sqrt{3})=\sqrt{10}+\sqrt{6}\)
b.
\(=\sqrt{\frac{(2-\sqrt{3})^2}{(2-\sqrt{3})(2+\sqrt{3})}}=\sqrt{\frac{(2-\sqrt{3})^2}{2^2-3}}=\sqrt{(2-\sqrt{3})^2}=|2-\sqrt{3}|=2-\sqrt{3}\)
Bài 3:
a.
\(M=\left[\frac{15(\sqrt{6}-1)}{(\sqrt{6}+1)(\sqrt{6}-1)}+\frac{4(\sqrt{6}+2)}{(\sqrt{6}-2)(\sqrt{6}+2)}-\frac{12(3+\sqrt{6})}{(3-\sqrt{6})(3+\sqrt{6})}\right](\sqrt{6}+11)\)
\(=\left[\frac{15(\sqrt{6}-1)}{6-1}+\frac{4(\sqrt{6}+2)}{6-2^2}-\frac{12(3+\sqrt{6})}{3^2-6}\right](\sqrt{6}+11)\)
\(=[3(\sqrt{6}-1)+2(\sqrt{6}+2)-4(3+\sqrt{6})](\sqrt{6}+11)=(\sqrt{6}-11)(\sqrt{6}+11)=6-11^2=-115\)
b.
\(N=\left[1-\frac{\sqrt{5}(\sqrt{5}+1)}{\sqrt{5}+1}\right].\left[\frac{\sqrt{5}(\sqrt{5}-1)}{1-\sqrt{5}}-1\right]\)
\(=(1-\sqrt{5})(-\sqrt{5}-1)=(\sqrt{5}-1)(\sqrt{5}+1)=5-1=4\)
Trục căn thức ở mẫu của biểu thức sau :
1 phần 1 cộng căn bậc hai cộng căn bậc ba (sr mik ko bt viết)
Trục căn thức và thực hiện phép tính : M = ( 15/√6 + 1 + 4/√6 - 2 - 12/3 - √6 ) ( √6 + 1 ) Giúp mik vs ạ
\(M=\left(\dfrac{15\left(\sqrt{6}-1\right)}{5}+\dfrac{4\left(\sqrt{6}+2\right)}{2}-\dfrac{12\left(3+\sqrt{6}\right)}{3}\right)\left(\sqrt{6}+1\right)\)
\(=\left(3\sqrt{6}-3+2\sqrt{6}+4-12-4\sqrt{6}\right)\left(\sqrt{6}+1\right)\)
\(=\left(\sqrt{6}-11\right)\left(\sqrt{6}+1\right)\)
\(=6+\sqrt{6}-11\sqrt{6}-11=-5-10\sqrt{6}\)
\(M=\left(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}\right)\left(\sqrt{6}+1\right)\)
\(M=\left[\dfrac{15\left(\sqrt{6}-1\right)}{\left(\sqrt{6}+1\right)\left(\sqrt{6}-1\right)}+\dfrac{4\left(\sqrt{6}+2\right)}{\left(\sqrt{6}+2\right)\left(\sqrt{6}-2\right)}-\dfrac{12\left(3+\sqrt{6}\right)}{\left(3+\sqrt{6}\right)\left(3-\sqrt{6}\right)}\right]\left(\sqrt{6}+1\right)\)
\(M=\left[\dfrac{15\left(\sqrt{6}-1\right)}{6-1}+\dfrac{4\left(\sqrt{6}+2\right)}{6-4}-\dfrac{12\left(3+\sqrt{6}\right)}{9-6}\right]\left(\sqrt{6}+1\right)\)
\(M=\left[3\left(\sqrt{6}-1\right)+2\left(\sqrt{6}+2\right)-4\left(3+\sqrt{6}\right)\right]\left(\sqrt{6}+1\right)\)
\(M=\left(3\sqrt{6}-3+2\sqrt{6}+4-12-4\sqrt{6}\right)\cdot\left(\sqrt{6}+1\right)\)
\(M=\left(5\sqrt{6}-4\sqrt{6}+1-12\right)\left(\sqrt{6}+1\right)\)
\(M=\left(\sqrt{6}-11\right)\left(\sqrt{6}+1\right)\)
\(M=6+\sqrt{6}-11\sqrt{6}-11\)
\(M=-10\sqrt{6}-5\)
trục căn thức ở mẫu rồi rút gọn

a) √8/(√5 - √3)
= 2√2.(√5 + √3)/[(√5 - √3)(√5 + √3)]
= 2√2(√5 + √3)/2
= √10 + √6
b) √[(2 - √3)/(2 + √3)]
= √{(2 - √3)²/[(2 + √3)(2 - √3)]}
= (2 - √3)/(4 - 3)
= 2 - √3
Lời giải:
a.
\(\frac{\sqrt{8}}{\sqrt{5}-\sqrt{3}}=\frac{\sqrt{8}(\sqrt{5}+\sqrt{3})}{(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})}=\frac{\sqrt{8}(\sqrt{5}+\sqrt{3})}{5-3}=\sqrt{2}(\sqrt{5}+\sqrt{3})=\sqrt{10}+\sqrt{6}\)
b.
\(\sqrt{\frac{2-\sqrt{3}}{2+\sqrt{3}}}=\sqrt{\frac{(2-\sqrt{3})^2}{(2+\sqrt{3})(2-\sqrt{3})}}=\sqrt{\frac{(2-\sqrt{3})^2}{2^2-3}}=\sqrt{(2-\sqrt{3})^2}=|2-\sqrt{3}|=2-\sqrt{3}\)
trục căn thức ở mẫu và thực hiện phép tính
4/(căn 5 - căn 2) + 3/ (căn 5 -2) -2/(căn 3-2) - (căn 3 -1)/6
\(\dfrac{4}{\sqrt{5}-\sqrt{2}}+\dfrac{3}{\sqrt{5}-2}-\dfrac{2}{\sqrt{3}-2}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{4\left(\sqrt{2}+\sqrt{5}\right)}{\left(\sqrt{5}-\sqrt{2}\right)\left(\sqrt{2}+\sqrt{5}\right)}+\dfrac{3\left(\sqrt{5}+2\right)}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}-\dfrac{2\left(\sqrt{3}+2\right)}{\left(\sqrt{3}-2\right)\left(\sqrt{3}+2\right)}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{4\left(\sqrt{2}+\sqrt{5}\right)}{\left(\sqrt{5}\right)^2-\left(\sqrt{2}\right)^2}+\dfrac{3\left(\sqrt{5}+2\right)}{\left(\sqrt{5}\right)^2-2^2}-\dfrac{2\left(\sqrt{3}+2\right)}{\left(\sqrt{3}\right)^2-2^2}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{4\left(\sqrt{2}+\sqrt{5}\right)}{3}+\dfrac{3\left(\sqrt{5}+2\right)}{1}-\dfrac{2\left(\sqrt{3}+2\right)}{-1}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{8\left(\sqrt{2}+\sqrt{5}\right)}{6}+\dfrac{18\left(\sqrt{5}+2\right)}{6}+\dfrac{12\left(\sqrt{3}+2\right)}{6}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{8\sqrt{2}+8\sqrt{5}+18\sqrt{5}+36+12\sqrt{3}+24-\sqrt{3}+1}{6}\)
\(=\dfrac{8\sqrt{2}+26\sqrt{5}+11\sqrt{3}+61}{6}\)
\(=\dfrac{4\left(\sqrt{5}+\sqrt{2}\right)}{3}+\dfrac{3\left(\sqrt{5}+2\right)}{1}+\dfrac{2\left(2+\sqrt{3}\right)}{1}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{4\sqrt{5}+4\sqrt{2}+9\sqrt{5}+18}{3}+\dfrac{4+2\sqrt{3}}{1}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{2\left(13\sqrt{5}+4\sqrt{2}+18\right)+24+12\sqrt{3}-\sqrt{3}+1}{6}\)
\(=\dfrac{26\sqrt{5}+4\sqrt{2}+36+25+11\sqrt{3}}{6}\)
\(=\dfrac{61+11\sqrt{3}+26\sqrt{5}+4\sqrt{2}}{6}\)
Mình sửa lại chút nha bạn
\(=\dfrac{4\left(\sqrt{5}+\sqrt{2}\right)}{3}+\dfrac{3\left(\sqrt{5}+2\right)}{1}+\dfrac{2\left(2+\sqrt{3}\right)}{1}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{4\sqrt{5}+4\sqrt{2}+9\sqrt{5}+18}{3}+\dfrac{4+2\sqrt{3}}{1}-\dfrac{\sqrt{3}-1}{6}\)
\(=\dfrac{2\left(13\sqrt{5}+4\sqrt{2}+18\right)+24+12\sqrt{3}-\sqrt{3}+1}{6}\)
\(=\dfrac{26\sqrt{5}+8\sqrt{2}+36+25+11\sqrt{3}}{6}\)
\(=\dfrac{61+11\sqrt{3}+26\sqrt{5}+8\sqrt{2}}{6}\)
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
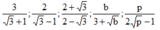
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
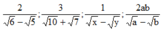
Một chất điểm chuyển động dọc theo trục 0x theo phương trình x = 2t + 1,5t^2 trong đó x tính bằng m; t tính bằng s. Gia tốc của chất điểm là A. 1,5 m/s2. B. -1,5 m/s. C. 3,0 m/s2. D. 3,5 m/s2. Lm ra lun nha, giúp mik vs mn T^T
\(x=2x+1.5t^2\)
Ta có :
\(\dfrac{1}{2}\cdot a=1.5\)
\(\Rightarrow a=1.5\cdot2=3\left(m\text{/}s^2\right)\)
a/ thực hiện phép tính: 5√75 -1/3√27
b/ trục căn thức ở mẫu: 12/3-√5
c/ tính giá trị biểu thức: √(√5-3)^2 +√5
a: \(=5\cdot5\sqrt{3}-\dfrac{1}{3}\cdot3\sqrt{3}=24\sqrt{3}\)
b: \(=\dfrac{12\left(3+\sqrt{5}\right)}{4}=9+3\sqrt{5}\)
c: \(=3-\sqrt{5}+\sqrt{5}=3\)