\(1,A=\left(\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\right)\cdot\dfrac{x-4}{\sqrt{x}}\\ =\dfrac{\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}}\\ =\dfrac{2\sqrt{x}}{\sqrt{x}}\\ =2\\ 2,A=\left(\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}\right):\dfrac{\sqrt{x}}{x-4}\\ =\dfrac{\sqrt{x}-2+\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{x-4}{\sqrt{x}}\\ =\dfrac{2\sqrt{x}}{x-4}\cdot\dfrac{x-4}{\sqrt{x}}\\ =\dfrac{2\sqrt{x}}{\sqrt{x}}\\ =2\\ 3,A=\left(\dfrac{x+3\sqrt{x}}{\sqrt{x}+3}-2\right)\left(\dfrac{x-1}{\sqrt{x}-1}+1\right)\\ =\left[\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\sqrt{x}+3}-2\right]\left[\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}-1}+1\right]\\ =\left(\sqrt{x}-2\right)\left(\sqrt{x}+1+1\right)\\ =\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\\ =\left(\sqrt{x}\right)^2-2^2\\ =x-4\)
Đúng 3
Bình luận (1)
Các câu hỏi tương tự
có ai biết giải bài này k hộ mình vs ( chi tiết hộ mình nhé )bài 1: trục căn thức ở mẫu và rút gọna, dfrac{1}{2sqrt{2}-3sqrt{3}}b, sqrt{dfrac{3-sqrt{5}}{3+sqrt{5}}}bài 2: trục căn thức ở mẫu và rút gọna, dfrac{sqrt{8}}{sqrt{5}-sqrt{3}}b, sqrt{dfrac{2-sqrt{3}}{2+sqrt{3}}}bài 3: trục căn thức và thực hiện phép tínha, Mleft(dfrac{15}{sqrt{6}+1}+dfrac{4}{sqrt{6}-2}-dfrac{12}{3-sqrt{6}}right).left(sqrt{6}+11right)b, N left(1-dfrac{5+sqrt{5}}{1+sqrt{5}}right).left(dfrac{5-sqrt{5}}{1-sqrt{5}}-1righ...
Đọc tiếp
có ai biết giải bài này k hộ mình vs ( chi tiết hộ mình nhé )
bài 1: trục căn thức ở mẫu và rút gọn
a, \(\dfrac{1}{2\sqrt{2}-3\sqrt{3}}\)
b, \(\sqrt{\dfrac{3-\sqrt{5}}{3+\sqrt{5}}}\)
bài 2: trục căn thức ở mẫu và rút gọn
a, \(\dfrac{\sqrt{8}}{\sqrt{5}-\sqrt{3}}\)
b, \(\sqrt{\dfrac{2-\sqrt{3}}{2+\sqrt{3}}}\)
bài 3: trục căn thức và thực hiện phép tính
a, M=\(\left(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}\right).\left(\sqrt{6}+11\right)\)
b, N= \(\left(1-\dfrac{5+\sqrt{5}}{1+\sqrt{5}}\right).\left(\dfrac{5-\sqrt{5}}{1-\sqrt{5}}-1\right)\)
Trục căn thức ở mẫu của biểu thức sau :
1 phần 1 cộng căn bậc hai cộng căn bậc ba (sr mik ko bt viết)
trục căn thức ở mẫu rồi rút gọn

Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
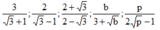
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
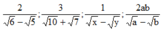
a/ thực hiện phép tính: 5√75 -1/3√27
b/ trục căn thức ở mẫu: 12/3-√5
c/ tính giá trị biểu thức: √(√5-3)^2 +√5
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
5
10
;
5
2
5
;
1
3
20
;
2
2
+
2
5
2
;
y
+
b...
Đọc tiếp
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
5 10 ; 5 2 5 ; 1 3 20 ; 2 2 + 2 5 2 ; y + b y b y
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
5
10
;
5
2
5
;
1
3
20
;
2
2
+
2
5
2...
Đọc tiếp
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa 5 10 ; 5 2 5 ; 1 3 20 ; 2 2 + 2 5 2 ; y + b y b y
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
2
6
-
5
;
3
10
+
7
;
1
x
-
y
;
2
a...
Đọc tiếp
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa 2 6 - 5 ; 3 10 + 7 ; 1 x - y ; 2 a b a - b
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
3
3
+
1
;
2
3
-
1
;
2
+
3
2
-
3
;
b...
Đọc tiếp
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa 3 3 + 1 ; 2 3 - 1 ; 2 + 3 2 - 3 ; b 3 + b ; p 2 p - 1










