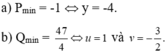Tìn giá trị nhỏ nhất của biểu thức sau : 4x2 + y2 - 12x + 8y+ 28

Những câu hỏi liên quan
Tìm giá trị nhỏ nhất của biểu thức sau:
\(\sqrt{4x2-4x+1}+\sqrt{4x2-12x+9}\)
Đặt \(C=\sqrt{4x^2-4x+1}+\sqrt{4x^2-12x+9}\)
\(=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(2x-3\right)^2}\)
\(=\left|2x-1\right|+\left|2x-3\right|\)
\(=\left|2x-1\right|+\left|3-2x\right|\)
\(\ge\left|\left(2x-1\right)+\left(3-2x\right)\right|=\left|2\right|=2\)
Vậy \(C_{min}=2\)
Đúng 0
Bình luận (0)
#)Giải :
\(\sqrt{4x^2-4x+1}+\sqrt{4x^2-12x+9}\)
\(=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(2x-3\right)^2}\)
\(=\left|2x-1\right|+\left|2x-3\right|\)
\(=\left|2x-1\right|+\left|3-2x\right|\ge\left|2x-1+3-2x\right|=2\)
Dấu ''='' xảy ra khi x = 1
Đúng 0
Bình luận (0)
\(\sqrt{4x^2-4x+1}+\sqrt{4x^2-12x+9}\)
\(=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(2x-3\right)^2}\)
\(=|2x-1|+|2x-3|\)
\(=|2x-1|+|3-2x|\ge|2x-1+3-2x|=2\)
Dấu"=" xảy ra \(\Leftrightarrow\left(2x-1\right)\left(3-2x\right)\ge0\Leftrightarrow\frac{1}{2}\le x\le\frac{3}{2}\)
Chỉ là góp ý:V
Đúng 0
Bình luận (1)
tìm giá trị nhỏ nhất của biểu thức sau : 4x2 + y2 - 12x +8y +28
\(A=4x^2+y^2-12x+8y+28\)
\(=\left(4x^2-12x+9\right)+\left(y^2+8y+16\right)+3\)
\(=\left[\left(2x\right)^2+2.2x.3+3^2\right]+\left(y^2+2.y.4+4^2\right)+3\)
\(=\left(2x+3\right)^2+\left(y+4\right)^2+3\)
Ta có :
\(\left(2x+3\right)^2\ge0\forall x\)
\(\left(y+4\right)^2\ge0\forall x\)
\(\Rightarrow\left(2x+3\right)^2+\left(y+4\right)^2+3\ge3\forall x\)
Dấu = xảy ra khi
\(\left\{{}\begin{matrix}\left(2x+3\right)^2=0\\\left(y+4\right)^2=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2x+3=0\\y+4=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{3}{2}\\y=-4\end{matrix}\right.\)
Vậy \(Min_A=3\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{2}{3}\\y=-4\end{matrix}\right.\)
Đúng 0
Bình luận (3)
Tìm giá trị nhỏ nhất của các biểu thức sau:
a) P = y 2 + 8y + 15;
b) Q = u 2 + y 2 – 2u + 3v + 15.
Tìm giá trị nhỏ nhất của các biểu thức.
a) M=x2+10x+28.
b) P=4x2-12x+10
Mình đang cần gấp ạ.Cảm ơn nhiều
Tìm giá trị nhỏ nhất của các biểu thức.
a) M=x2+10x+28.
b) P=4x2-12x+10
Mình đang cần gấp ạ.Cảm ơn nhiều
a) \(M=x^2+10x+28=\left(x^2+10+25\right)+3=\left(x+5\right)^2+3\ge3\)
\(minM=3\Leftrightarrow x=-3\)
b) \(P=4x^2-12x+10=\left(4x^2-12x+9\right)+1=\left(2x-3\right)^2+1\ge1\)
\(minP=1\Leftrightarrow x=\dfrac{3}{2}\)
Đúng 1
Bình luận (1)
Tính giá trị nhỏ nhất của các biểu thức sau:
a) A = 4x2 +4x + 11
b) C = x2 - 2x + y2 - 4y + 7
Lời giải:
a)
$A=4x^2+4x+11=(4x^2+4x+1)+10=(2x+1)^2+10\geq 10$
Vậy $A_{\min}=10$. Giá trị này đạt tại $(2x+1)^2=0$
$\Leftrightarrow x=-\frac{1}{2}$
b)
$C=x^2-2x+y^2-4y+7=(x^2-2x+1)+(y^2-4y+4)+2$
$=(x-1)^2+(y-2)^2+2\geq 2$
Vậy $C_{\min}=2$. Giá trị này đạt tại $(x-1)^2=(y-2)^2=0$
$\Leftrightarrow x=1; y=2$
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất, nhỏ nhất của biểu thức:
1) A= x2 - 6x +5
2) B= 4x2 + 1 + 18x
3) C= 9 - y2 - 4y
4) D= x2 - 8
1:
=x^2-6x+9-4=(x-3)^2-4>=-4
Dấu = xảy ra khi x=3
3: =-y^2-4y-4+13
=-(y+2)^2+13<=13
Dấu = xảy ra khi y=-2
4: D=x^2-8>=-8
Dấu = xảy ra khi x=0
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất hoặc nhỏ nhất của biểu thức:
a) A = x2-4x+20
b) B = x2+3x+7
c) C = -x2-10x+70
d) D = -4x2+12x+1
\(A=x^2-4x+20=x^2-4x+4+16=\left(x-2\right)^2+16\)
Do \(\left(x-2\right)^2\ge0\)
\(\Rightarrow\left(x-2\right)^2+16\ge16\)
\(\Rightarrow Min\left(A\right)=16\)
\(B=x^2-3x+7=x^2-3x+\dfrac{9}{4}-\dfrac{9}{4}+7=\left(x-\dfrac{3}{2}\right)^2+\dfrac{19}{4}\)
Do \(\left(x-\dfrac{3}{2}\right)^2\ge0\)
\(\Rightarrow\left(x-\dfrac{3}{2}\right)^2+\dfrac{19}{4}\ge\dfrac{19}{4}\)
\(\Rightarrow Min\left(B\right)=\dfrac{19}{4}\)
\(C=-x^2-10x+70=-\left(x^2+10x+25\right)+25+70=-\left(x-5\right)^2+95\)
Do \(-\left(x-5\right)^2\le0\)
\(\Rightarrow-\left(x-5\right)^2+95\le95\)
\(\Rightarrow Max\left(C\right)=95\)
\(D=-4x^2+12x+1=-\left(4x^2-12x+9\right)+9+1=-\left(2x-3\right)^2+10\)
Do \(-\left(2x-3\right)^2\le0\)
\(\Rightarrow-\left(2x-3\right)^2+10\le10\)
\(\Rightarrow Max\left(D\right)=10\)
Đúng 3
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức
C = 2x2 + 2y2 + 26 + 12x - 8y
C = 2x2 + 2y2 + 26 + 12x - 8y
C = (2x2 + 12x + 18) + (2y2 - 8y + 8)
C = 2(x2 + 6x + 9) + 2(y2 - 4y + 4)
C = 2(x + 3)2 + 2(y - 2)2 \(\ge\)0 với mọi x;y
Dấu "=" xảy ra <=> x + 3 = 0 và y - 2 = 0
<=> x = -3 và y = 2
Vậy MinC = 0 khi x = -3 và y = 2
\(C=2\left(x^2+6x+9\right)+2\left(y^2-4y+4\right)=2\left(x+3\right)^2+2\left(y-2\right)^2\ge0\)
Vậy MIN C=0 khi và chỉ khi x+3=y-2=0 suy ra x=-3;y=2
C = 2x2 + 2y2 + 26 + 12x - 8y
C = ( 2x2 + 12x + 18 ) + ( 2y2 - 8y + 8 )
C = 2( x2 + 6x + 9 ) + 2( y2 - 4y + 4 )
C = 2( x + 3 )2 + 2( y - 2 )2
\(\hept{\begin{cases}2\left(x+3\right)^2\ge0\forall x\\2\left(y-2\right)^2\ge0\forall y\end{cases}}\Rightarrow2\left(x+3\right)^2+2\left(y-2\right)^2\ge0\forall x,y\)
Đẳng thức xảy ra <=> \(\hept{\begin{cases}x+3=0\\y-2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-3\\y=2\end{cases}}\)
Vậy CMin = 0 , đạt được khi x = -3 , y = 2
Xem thêm câu trả lời