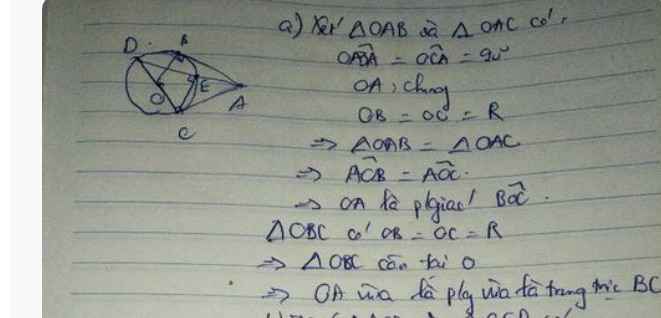Từ điểm E ở ngoài đường tròn (O; R) kẻ hai tiếp tuyến EI và EK tới đường tròn (O).
Chứng minh rằng: 4 điểm E, I, O, K cùng thuộc 1 đường tròn

Những câu hỏi liên quan
Từ điểm E ở ngoài đường tròn (O; R) kẻ hai tiếp tuyến EI và EK tới đường tròn (O).
Chứng minh rằng: 4 điểm E, I, O, K cùng thuộc 1 đường tròn
cho đường tròn(o;r), từ điểm a ở bên ngoài đường tròn kẻ 2 tiếp tuyến ab, ac với đường tròn(o) (b,c là tiếp điểm) từ b kẻ đường thẳng song song ac cắt đường tròn(o) tại d(d khác b), đường thẳng ad cắt đường tròn (o) tại e( e khác d) a) chứng minh tứ giác aboc nội tiếp b) chứng minh ab²= ae×ad c) giả sử oa=2r. Tính góc bec và diện tích obac d) so sánh góc cea và góc bec
a) Xét tứ giác ABOC có
\(\widehat{ABO}\) và \(\widehat{ACO}\) là hai góc đối
\(\widehat{ABO}+\widehat{ACO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 1
Bình luận (0)
Từ điểm A nằm ngoài đường tròn ( O ; R ) với OA > 2R , kẻ các tiếp tuyến AB , AC của đường tròn ( O ) ( B , C là các tiếp điểm ) . Vẽ đường kính BD của đường tròn ( O ) ; AD cắt đường tròn ( O ) ở E ( E khác D ) . a ) Chứng minh : OAI BC tại H và 0A // DC . b ) Chứng minh : AE.AD = AH.AO. c ) Gọi I là trung điểm HA . Chứng minh tam giác AIB đồng dạng với tam giác DHB .
Từ điểm A ở ngoài đường tròn (O) vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Vẽ đường kính BD của đường tròn (O). Đoạn AD cắt đường tròn (O) tại E (E khác D). Gọi I là trung điểm của ED, H là giao điểm của AO và BC.a) Chứng minh tứ giác ABOC nội tiếp được đường tròn.b) Chứng minh: IE2 + AH.AO AI2.c) Gọi K là chân đường vuông góc kẻ từ C đến OD. Đoạn ED cắt CK tại M. Chứng minh M là trung điểm của CK.giải giúp mình câu b và c với ạ, mình cảm ơn
Đọc tiếp
Từ điểm A ở ngoài đường tròn (O) vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Vẽ đường kính BD của đường tròn (O). Đoạn AD cắt đường tròn (O) tại E (E khác D). Gọi I là trung điểm của ED, H là giao điểm của AO và BC.
a) Chứng minh tứ giác ABOC nội tiếp được đường tròn.
b) Chứng minh: IE2 + AH.AO = AI2.
c) Gọi K là chân đường vuông góc kẻ từ C đến OD. Đoạn ED cắt CK tại M. Chứng minh M là trung điểm của CK.
giải giúp mình câu b và c với ạ, mình cảm ơn
Cho đường tròn (O) điểm M nằm bên ngoài đường tròn, từ M kẻ tiếp tuyến MA (A là tiếp điểm) và cát tuyến MBC tới đường tròn, Phân giác của góc BAC cắt BC ở D, cắt đường tròn ở E. Cm
a, MA=MD
b, AD.AE=AC.AB
Cho đường tròn (O) và điểm S nằm bên ngoài đường tròn. Từ S kẻ tiếp tuyến SA và cát tuyến SBC tới đường tròn. Phân giác của góc BAC cắt BC ở D, cắt đường tròn ở E. Kẻ tiếp tuyến SA’ với đường tròn (O). Gọi H là giao điểm OS và AA’ , G là giao của OE và BS; F là giao của AA’ với BC. Trên tia AC lấy điểm Q sao cho AQ AB. Chứng minh AO vuông góc DQ.
Đọc tiếp
Cho đường tròn (O) và điểm S nằm bên ngoài đường tròn. Từ S kẻ tiếp tuyến SA và cát tuyến SBC tới đường tròn. Phân giác của góc BAC cắt BC ở D, cắt đường tròn ở E. Kẻ tiếp tuyến SA’ với đường tròn (O). Gọi H là giao điểm OS và AA’ , G là giao của OE và BS; F là giao của AA’ với BC. Trên tia AC lấy điểm Q sao cho AQ = AB. Chứng minh AO vuông góc DQ.
Từ điểm A nằm ngoài đường tròn (O), vẽ cát tuyến ABC với đường tròn. Các tiếp tuyến của đường tròn tại B và C cắt nhau ở K. Qua K kẻ đường thẳng vuông góc với AO, cắt AO tại H và đường tròn (O) tại E và F (E nằm giữa K và F). Gọi M là giao điểm của OK và BC.gọi D là giao điểm của BC và EF chứng minh DB.AC =DC.AB
4/ Từ một điểm A ở ngoài đường tròn (O;R) vẽ tiếp tuyến AB và cát tuyển ACD
a) CM : AB2=AC. AD
b) Gọi I là trung điễm CD. CM: tứ giác ABOI nội tiếp đường tròn (K), xác định K.
c) Đường tròn (K) cắt đường tròn (O) tại điểm E (E khác A).
CM : AE là tiếp tuyến của đường tròn (O)
Xem chi tiết
Từ điểm A ở bên ngoài đường tròn (O), kẻ 2 tiếp tuyến AB và AC đến đường tròn (O) (B, C là tiếp điểm). Kẻ cát tuyến ADE vs đường tròn (O) (D nằm giữa A và E).
a) Cm: 4 điểm A, B, O, C cùng thuộc một đường tròn
b) Cm OA ⊥ BC tại H và OD² = OH × OA. Từ đó suy ra tam giác OHD đồng dạng vs tam giác ODA.
Giải và vẽ hình giúp mình vớiii !! :(
a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,C,O cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
mà OB=OD
nên \(OD^2=OH\cdot OA\)
=>\(\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
Xét ΔODA và ΔOHD có
\(\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
\(\widehat{DOA}\) chung
Do đó: ΔODA đồng dạng với ΔOHD
Đúng 1
Bình luận (0)