lớp 8 có pt bậc 2 ak??

\(m,x^2+6x-16=0\)

\(\Leftrightarrow x^2-2x+8x-16=0\)

\(\Leftrightarrow x\left(x-2\right)+8\left(x-2\right)=0\)

\(\Leftrightarrow\left(x+8\right)\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+8=0\\x-2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-8\\x=2\end{matrix}\right.\)

\(n,2x^2+5x-3=0\)

\(\Leftrightarrow2x^2-x+6x-3=0\)

\(\Leftrightarrow x\left(2x-1\right)+3\left(2x-1\right)=0\)

\(\Leftrightarrow\left(x+3\right)\left(2x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\2x-1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=\dfrac{1}{2}\end{matrix}\right.\)

\(k,x\left(2x-7\right)-4x+14=0\)

\(\Leftrightarrow2x^2-4x-7x+14=0\)

\(\Leftrightarrow2x\left(x-2\right)-7\left(x-2\right)=0\)

\(\Leftrightarrow\left(2x-7\right)\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-7=0\\x-2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=2\end{matrix}\right.\)

Đặt \(2x^2+x-213=a;x^2-5x-2012=b\)

Khi đó phương trình tương đương với:

\(a^2+4b^2=4ab\)

\(\Leftrightarrow\left(a-2b\right)^2=0\)

\(\Leftrightarrow a-2b=0\)

\(\Leftrightarrow a=2b\)

Đến đây dễ rồi

Lần sao bạn ấn vào Latex để gõ các công thức như thế nào để câu hỏi được rõ hơn nha. Kí hiệu \(\sum\) ở trên thanh công cụ nhé.

Giải:

ĐKXĐ: \(3-2x\ge0\Leftrightarrow3\ge2x\Leftrightarrow x\le\dfrac{3}{2}\)

\(\sqrt{x^2-6x+9}=3-2x\)

\(\Leftrightarrow x^2-6x+9=\left(3-2x\right)^2\\ \Leftrightarrow x^2-6x+9=9-12x+4x^2\\ \Leftrightarrow3x^2-6x=0\\ \Leftrightarrow3x\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=2\left(ktm\right)\end{matrix}\right.\)

Vậy x = 0

\(\sqrt{x^{ }2-6x+9}=4-x\)
\(\sqrt{\left(x-3\right)^{ }2}=4-x\)
x-3=4-x
x+x=4+3
2x=7
x=\(\dfrac{7}{2}\)

Lời giải:
a.

PT \(\Leftrightarrow \left\{\begin{matrix} 4-x\geq 0\\ x^2-6x+9=(4-x)^2=x^2-8x+16\end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} x\leq 4\\ 2x=7\end{matrix}\right.\Leftrightarrow x=\frac{7}{2}\)

b.

ĐKXĐ: $x\geq \frac{3}{2}$

PT \(\Leftrightarrow \sqrt{(2x-3)+2\sqrt{2x-3}+1}+\sqrt{(2x-3)+8\sqrt{2x-3}+16}=5\)

\(\Leftrightarrow \sqrt{(\sqrt{2x-3}+1)^2}+\sqrt{(\sqrt{2x-3}+4)^2}=5\)

\(\Leftrightarrow |\sqrt{2x-3}+1|+|\sqrt{2x-3}+4|=5\)

\(\Leftrightarrow \sqrt{2x-3}+1+\sqrt{2x-3}+4=2\sqrt{2x-3}+5=5\)

\(\Leftrightarrow \sqrt{2x-3}=0\Leftrightarrow x=\frac{3}{2}\)

a: Ta có: \(\sqrt{x^2-6x+9}=4-x\)

\(\Leftrightarrow\left|x-3\right|=4-x\)

\(\Leftrightarrow\left[{}\begin{matrix}x-3=4-x\left(x\ge3\right)\\x-3=x-4\left(x< 3\right)\left(loại\right)\end{matrix}\right.\)

\(\Leftrightarrow2x=7\)

hay \(x=\dfrac{7}{2}\left(nhận\right)\)

\(2x^2-6x-3=0\)

\(\Delta'=3^2+3.2=15>0\)

⇒ Phương trình có hai nghiệm phân biệt.

Theo hệ thức viét có : \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=-\dfrac{3}{2}\end{matrix}\right.\)

Ta có : \(A=x_1^2x_2^2-2x_1-2x_2=\left(x_1x_2\right)^2-2\left(x_1+x_2\right)=\left(-\dfrac{3}{2}\right)^2-2.3=-\dfrac{15}{4}\)

Vậy \(A=-\dfrac{15}{4}\) thì thỏa mãn điều kiện bài ra.

\(pt\Leftrightarrow\sqrt{\left(x^4-9\right)+\left(x^3-3x\right)}+\sqrt{\left(x^4-9\right)+\left(2x^3-6x\right)}+\sqrt{x^2-3}=0\)

\(\Leftrightarrow\sqrt{\left(x^2-3\right)\left(x^2+x+3\right)}+\sqrt{\left(x^2-3\right)\left(x^2+2x+3\right)}+\sqrt{x^2-3}=0\)

\(\Leftrightarrow\sqrt{x^2-3}\left(\sqrt{x^2+x+3}+\sqrt{x^2+2x+3}+1\right)=0\)

\(\text{Nếu }x=\pm\sqrt{3}\Rightarrow\text{thỏa mãn còn lại thì thừa số số 2}>0\text{ nên không thỏa}\)

\(a)x^2-9x+20=0 \\<=>(x-4)(x-5)=0 \\<=>x=4\ hoặc\ x=5 \\b)x^2-3x-18=0 \\<=>(x+3)(x-6)=0 \\<=>x=-3\ hoặc\ x=6 \\c)2x^2-9x+9=0 \\<=>(x-3)(2x-3)=0 \\<=>x=3\ hoặc\ x=\dfrac{3}{2}\)

d: \(\Leftrightarrow3x^2-6x-2x+4=0\)

=>(x-2)(3x-2)=0

=>x=2 hoặc x=2/3

e: \(\Leftrightarrow3x\left(x^2-2x-3\right)=0\)

=>x(x-3)(x+1)=0

hay \(x\in\left\{0;3;-1\right\}\)

f: \(\Leftrightarrow x^2-5x-2+x=0\)

\(\Leftrightarrow x^2-4x-2=0\)

\(\Leftrightarrow\left(x-2\right)^2=6\)

hay \(x\in\left\{\sqrt{6}+2;-\sqrt{6}+2\right\}\)

ĐKXĐ: x ≠ - 1;x ≠ 3.

Ta có: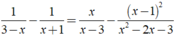

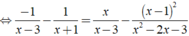
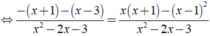
⇔ -2x + 2 = 3x - 1

⇔ 5x = 3 ⇔ x = 3/5.

Kết hợp điều kiện, vậy phương trình đã cho có nghiệm là x = 3/5.