Rút gọn về phân số tối giản:
b) \(\dfrac{50}{125}\)
Rút gọn về phân số tối giản: a) \(\frac{{90}}{{27}}\); b) \(\frac{{50}}{{125}}\).
a) Ta có: \(90 = 2.3^2.5; 27 = 3^3\)
Thừa số nguyên tố chung là 3 với số mũ nhỏ nhất là 2 nên \(ƯCLN (90, 27) = 3^2 = 9\)
\(\dfrac{{90}}{{27}} = \dfrac{{90:9}}{{27:9}} = \dfrac{{10}}{3}\)
b) Ta có: \(50 = 2.5^2 ;125 = 5^3\)
Thừa số nguyên tố chung là 5 với số mũ nhỏ nhất là 2 nên \(ƯCLN(50, 125) =5^2= 25\)
\(\dfrac{{50}}{{125}} = \dfrac{{50:25}}{{125:25}} = \dfrac{2}{5}\)
Các phân số sau đã là phân số tối giản chưa? Nếu chưa, hãy rút gọn về phân số tối giản:
a) \(\dfrac{{50}}{{85}};\) b) \(\dfrac{{23}}{{81}}\).
a) \(\dfrac{{50}}{{85}}\)
Ta có: \(50 =2.5^2; 85= 5.17\)
Thừa số nguyên tố chung là 5 với số mũ nhỏ nhất là 1 nên ƯCLN(50, 85) = 5. Do đó, \(\dfrac{{50}}{{85}}\) chưa là phân số tối giản
Ta có: \(\dfrac{{50}}{{85}} = \dfrac{{50:5}}{{85:5}} = \dfrac{{10}}{{17}}\)
b)\(\dfrac{{23}}{{81}}\)
Ta có: \(23 = 23; 81 = 3^4\)
Chúng không có thừa số nguyên tố chung nên ƯCLN(23, 81) = 1. Do đó, \(\dfrac{{23}}{{81}}\) là phân số tối giản.
Rút gọn các phân số sau về phân số tối giản: \(\dfrac{60}{72};\dfrac{70}{95};\dfrac{150}{360}.\)
\(\dfrac{60}{72}=\dfrac{60:12}{72:12}=\dfrac{5}{6}\\ \dfrac{70}{95}=\dfrac{70:5}{95:5}=\dfrac{14}{19}\\ \dfrac{150}{360}=\dfrac{150:30}{360:30}=\dfrac{5}{12}\)
\(\dfrac{60}{72}=\dfrac{5}{6}\)
\(\dfrac{70}{95}=\dfrac{14}{19}\)
\(\dfrac{150}{360}=\dfrac{5}{12}\)
Các phân số sau đã là phân số tối giản chưa? Nếu chưa, hãy rút gọn về phân số tối giản.
a) \(\dfrac{27}{123}\);
b) \(\dfrac{33}{77}\).
a) Phân số đã cho chưa tối giản
\(\dfrac{27}{123}=\dfrac{9\cdot3}{41\cdot3}=\dfrac{9}{41}\)
b) Phân số đã cho chưa tối giản
\(\dfrac{33}{77}=\dfrac{3\cdot11}{7\cdot11}=\dfrac{3}{7}\)
a, \(\dfrac{27}{123}=\dfrac{9}{41}\)
b, \(\dfrac{33}{77}=\dfrac{3}{7}\)
Rút gọn mỗi phân số sau về phân số tối giản:
\(\dfrac{14}{21};\dfrac{-36}{48};\dfrac{28}{-52};\dfrac{-54}{-90}.\)
\(\dfrac{14}{21}=\dfrac{7\cdot2}{7\cdot3}=\dfrac{2}{3}\)
\(\dfrac{-36}{48}=\dfrac{-12\cdot3}{12\cdot4}=-\dfrac{3}{4}\)
\(\dfrac{28}{-52}=\dfrac{7\cdot4}{-4\cdot13}=-\dfrac{7}{13}\)
\(\dfrac{-54}{-90}=\dfrac{-18\cdot3}{-18\cdot5}=\dfrac{3}{5}\)
\(\dfrac{14}{21}\) =\(\dfrac{2}{3}\)
\(\dfrac{-36}{48}\) =\(\dfrac{3}{4}\)
\(\dfrac{28}{-52}\)=\(\dfrac{7}{-13}\)
\(\dfrac{-54}{-90}\) =\(\dfrac{6}{9}=\dfrac{2}{3}\)
\(\dfrac{14}{21}=\dfrac{2}{3}\)
\(\dfrac{-36}{48}=-\dfrac{3}{4}\)
\(\dfrac{28}{-52}=-\dfrac{7}{13}\)
\(\dfrac{-54}{-90}=\dfrac{3}{5}\)
Câu 10: Rút gọn mỗi phân số sau về phân số tối giản: \(\dfrac{8}{-12}\dfrac{400}{700}\dfrac{-10}{6}\dfrac{-35}{-105}\)
\(\dfrac{8}{-12}=\dfrac{-8}{12}=\dfrac{-2}{3}\)
\(\dfrac{400}{700}=\dfrac{4}{7}\)
\(\dfrac{-10}{6}=\dfrac{-5}{3}\)
\(\dfrac{-35}{-105}=\dfrac{35}{105}=\dfrac{1}{3}\)
Rút gọn các phân số sau về phân số tối giản:
a) \(\dfrac{8}{16}\) b) \(\dfrac{10}{30}\) c) \(\dfrac{24}{18}\) d) \(\dfrac{20}{28}\)
a) \(\dfrac{8}{16}=\dfrac{8:8}{16:8}=\dfrac{1}{2}\)
b) \(\dfrac{10}{30}=\dfrac{10:10}{30:10}=\dfrac{1}{3}\)
c) \(\dfrac{24}{18}=\dfrac{24:6}{18:6}=\dfrac{4}{3}\)
d) \(\dfrac{20}{28}=\dfrac{20:4}{28:4}=\dfrac{5}{7}\)
a) Quan sát cách tính của Hiếu và Thảo khi rút gọn phân số \(\dfrac{12}{18}\) rồi nêu nhận xét:
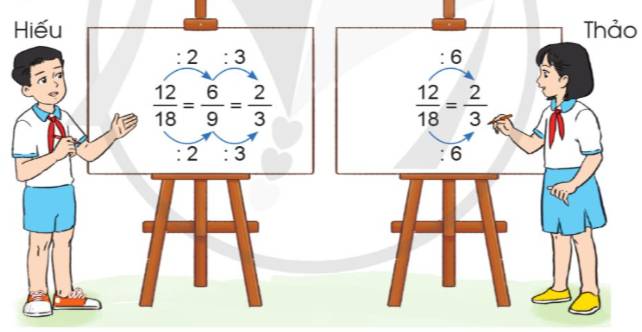
b) Rút gọn phân số \(\dfrac{30}{60}\) về dạng phân số tối giản sử dụng cách làm của Hiếu hoặc của Thảo.
a) Cách rút gọn của Thảo nhanh hơn còn của Hiếu thì lâu hơn vì phải làm nhiều bước
b) Sử dụng cách của Hiếu:
\(\dfrac{30}{60}=\dfrac{30:10}{60:10}=\dfrac{3}{6}=\dfrac{3:3}{6:3}=\dfrac{1}{2}\)
Sử dụng cách của Thảo:
\(\dfrac{30}{60}=\dfrac{30:30}{60:30}=\dfrac{1}{2}\)
rút gọn phân số
\(\dfrac{72\times75}{125\times108}\)
rút gọn bằng cách nhanh nhất
\(\dfrac{72\times75}{125\times108}\) = \(\dfrac{36\times2\times25\times3}{25\times5\times36\times3}\) = \(\dfrac{2}{5}\)