Cho (O) M nằm ngoài đường tròn vẽ 2 tt MA, MB . H là giao điểm AB và MO
a) cm M ,A,O,B thuộc một đường tròn

Những câu hỏi liên quan
cho đường tròn O và điểm M nằm ngoài đường tròn O . từ điểm M vẽ 2 tiếp tuyến MA ,MB của đường tròn . từ điểm M vẽ 2 tiếp tuyến MA , MB của đường tròn O .gọi H là giao điểm của MO và AB .Qua M vẽ cát tuyến MCD của đường tròn O (, D thuộc đường tròn O) sao cho đường thẳng MD cắt đoạn thẳng HB . gọi I là trung điểm dây cung CDA/ chứng minh OI vuông góc CD tại I và tứ giác MAOI nội tiếpB/ chứng minh MA2 MC.MD và tứ giác OHCD nội tiếpC/ trên cung nhỏ AD lấy điểm N sao cho DNBD . qua C vẽ đường thẳng...
Đọc tiếp
cho đường tròn O và điểm M nằm ngoài đường tròn O . từ điểm M vẽ 2 tiếp tuyến MA ,MB của đường tròn . từ điểm M vẽ 2 tiếp tuyến MA , MB của đường tròn O .gọi H là giao điểm của MO và AB .Qua M vẽ cát tuyến MCD của đường tròn O (, D thuộc đường tròn O) sao cho đường thẳng MD cắt đoạn thẳng HB . gọi I là trung điểm dây cung CD
A/ chứng minh OI vuông góc CD tại I và tứ giác MAOI nội tiếp
B/ chứng minh MA2 =MC.MD và tứ giác OHCD nội tiếp
C/ trên cung nhỏ AD lấy điểm N sao cho DN=BD . qua C vẽ đường thẳng song song với DN cắt đường thẳng MN tại E và cũng qua C vẽ đường thẳng song song viws BD cắt cạnh A tại F . chứng minh CEF cân
câu này hơi dài , cảm ơn mấy bạn vì công đọc , sai thì thôi, đúng thì ok , nhưng cảm ơn mn vì đọc cái bài dài này nhá :))
cho đường tròn O và điểm M nằm ngoài đường tròn O . từ điểm M vẽ 2 tiếp tuyến MA ,MB của đường tròn . từ điểm M vẽ 2 tiếp tuyến MA , MB của đường tròn O .gọi H là giao điểm của MO và AB .Qua M vẽ cát tuyến MCD của đường tròn O (, D thuộc đường tròn O) sao cho đường thẳng MD cắt đoạn thẳng HB . gọi I là trung điểm dây cung CDB/ chứng minh MA2 MC.MD và tứ giác OHCD nội tiếpC/ trên cung nhỏ AD lấy điểm N sao cho DNBD . qua C vẽ đường thẳng song song với DN cắt đường thẳng MN tại E và cũng qua C vẽ...
Đọc tiếp
cho đường tròn O và điểm M nằm ngoài đường tròn O . từ điểm M vẽ 2 tiếp tuyến MA ,MB của đường tròn . từ điểm M vẽ 2 tiếp tuyến MA , MB của đường tròn O .gọi H là giao điểm của MO và AB .Qua M vẽ cát tuyến MCD của đường tròn O (, D thuộc đường tròn O) sao cho đường thẳng MD cắt đoạn thẳng HB . gọi I là trung điểm dây cung CD
B/ chứng minh MA2 =MC.MD và tứ giác OHCD nội tiếp
C/ trên cung nhỏ AD lấy điểm N sao cho DN=BD . qua C vẽ đường thẳng song song với DN cắt đường thẳng MN tại E và cũng qua C vẽ đường thẳng song song viws BD cắt cạnh A tại F . chứng minh CEF cân
b: Xét ΔMAC và ΔMDA có
góc MAC=góc MDA
góc AMC chung
=>ΔMAC đồng dạng với ΔMDA
=>MA^2=MC*MD=MH*MO
=>MC/MO=MH/MD
=>ΔMCH đồng dạng với ΔMOD
=>góc MCH=góc MOD
=>góc HOD+góc HCD=180 độ
=>HODC nội tiếp
Đúng 0
Bình luận (0)
Cho (O;R) và một điểm M nằm ngoài (O). Từ M vẽ 2 tiếp tuyến MA, MB và cát tuyến MCD với đường tròn(MC<MD, tia MC nằm giữa 2 tia MA và MO). I là trung điểm của CD, H là giao điểm của AB và OM
a) C/m 5 điểm A, M, I, O, B cùng thuộc 1 đường tròn, xác định tâm của đường tròn đó
b) C/m IM là tia phân giác góc AIB
a) tứ giác AOBM nội tiếp thì có tâm đường tròn là trung điểm OM
cần CM tứ giác OIMB nội tiếp: dùng tổng hai góc đối cộng với nhau bằng 180o, mà đã có OBM=90o, mà I là trung điểm dây cung CD nên OI vuông góc CD luôn => OIM=90o
Vậy tứ giác OIMB nội tiếp thì tâm đường tròn cũng tại trung điểm OM luôn
b) 5 điểm A,I,O,B,M cùng thuộc 1 đtron
=> tứ giác AIOB nội tiếp => góc AIB=AOB (cùng chắn cung)
tứ giác AIOM nội tiếp => góc AIM=AOM (ccc)
mà góc AOM=1/2AOB=AIM=1/2AIB
=> BIM=1/2AIB (đpcm
Đúng 0
Bình luận (0)
Cho điểm M nằm ngoài đường tròn (O;R). Qua M vẽ hai tiếp tuyến MA, MB và cát tuyến MCD (A,B,C,D thuộc đường tròn tâm O), tia MC nằm giữa hai tia MO và MA. Gọi H là giao điểm của AB và MO.a/ CM tứ giác MAOB nội tiếp.b/ Gọi K là trung điểm CD. Chứng minh 5 điểm M, A, K, O, B cùng thuộc một đường tròn. Từ đó suy ra KM là phân giác của góc AKB.c/ Đường thẳng OK cắt đường thẳng AB tại N. Chứng minh ND là tiếp tuyến đường tròn (O)
Đọc tiếp
Cho điểm M nằm ngoài đường tròn (O;R). Qua M vẽ hai tiếp tuyến MA, MB và cát tuyến MCD (A,B,C,D thuộc đường tròn tâm O), tia MC nằm giữa hai tia MO và MA. Gọi H là giao điểm của AB và MO.
a/ CM tứ giác MAOB nội tiếp.
b/ Gọi K là trung điểm CD. Chứng minh 5 điểm M, A, K, O, B cùng thuộc một đường tròn. Từ đó suy ra KM là phân giác của góc AKB.
c/ Đường thẳng OK cắt đường thẳng AB tại N. Chứng minh ND là tiếp tuyến đường tròn (O)
cho điểm m nằm ngoài đường tròn (O;R).Kẻ các tiếp tuyến MA,MB với đường tròn (O) (A,B là các tiếp điểm ).Vẽ đường kính AD của đường tròn(O).Gọi H là giao điểm của MO và AB.a/Chứng minh rằng :MO vuông góc AB tại Hb/Cho biết R 15 cm và MO 25 cm .Tính độ dài đoạn OH. c/ Gọi G là giao điểm của BD và AM .Chứng minh :AM MG.d/ Gọi I là giao điểm của tia OM và đường tròn (O). Chứng minh I là tâm đường tròn nội tiếp tam giác MAB . Tính độ dài đoạn thẳng BD theo R ,r với r là bán kính của đường tròn nộ...
Đọc tiếp
cho điểm m nằm ngoài đường tròn (O;R).Kẻ các tiếp tuyến MA,MB với đường tròn (O) (A,B là các tiếp điểm ).Vẽ đường kính AD của đường tròn(O).Gọi H là giao điểm của MO và AB.
a/Chứng minh rằng :MO vuông góc AB tại H
b/Cho biết R = 15 cm và MO = 25 cm .Tính độ dài đoạn OH.
c/ Gọi G là giao điểm của BD và AM .Chứng minh :AM = MG.
d/ Gọi I là giao điểm của tia OM và đường tròn (O). Chứng minh I là tâm đường tròn nội tiếp tam giác MAB . Tính độ dài đoạn thẳng BD theo R ,r với r là bán kính của đường tròn nội tiếp tam giác MAB.
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO\(\perp\)AB
Đúng 0
Bình luận (0)
Cho đường tròn tâm O, bán kính R. Từ điểm M nằm ngoài đường tròn vẽ các tiếp tuyến MA, MB ( A, B thuộc (O)). Vẽ cát tuyến MCD không đi qua O (C nằm giữa M và D). Gọi H là trung điểm dây CD
a. CM các điểm M,A,O,H,B cùng thuộc 1 đg tròn
b. CM: MC.MD=MO2-R2
c. Tia BH cắt (O) tại F. CM AF song song CD
a: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=180^0\)
nên MAOB là tứ giác nội tiếp(1)
Xét tứ giác OHMB có \(\widehat{OHM}+\widehat{OBM}=180^0\)
nên OHMB là tứ giác nội tiếp(2)
Từ (1) và (2) suy ra O,H,A,M,B cùng thuộc đường tròn
b: Xét ΔMAC và ΔMDA có
\(\widehat{MAC}=\widehat{MDA}\)
\(\widehat{AMC}\) chung
Do đó:ΔMAC\(\sim\)ΔMDA
Suy ra: MA/MD=MC/MA
hay \(MA^2=MD\cdot MC=MO^2-R^2\)
Đúng 3
Bình luận (1)
Cho (O) và một điểm M nằm ngoài đường tròn. Từ M kẻ 2 tiếp tuyến MA,MB với đường tròn (O) (A và B là 2 tiếp điểm). Gọi I là giao điểm của OM và AB. Kẻ đường kính BC của đường tròn (O).a,C/m 4 điểm M,A,O,B cùng thuộc một đường tròn.b,C/m OI.OMOA2c,Qua O vẽ đường thẳng vuông góc với MC tại E và cắt đường thẳng BA tại F. C/m FC là tiếp tuyến của đường tròn (O)
Đọc tiếp
Cho (O) và một điểm M nằm ngoài đường tròn. Từ M kẻ 2 tiếp tuyến MA,MB với đường tròn (O) (A và B là 2 tiếp điểm). Gọi I là giao điểm của OM và AB. Kẻ đường kính BC của đường tròn (O).
a,C/m 4 điểm M,A,O,B cùng thuộc một đường tròn.
b,C/m OI.OM=OA2
c,Qua O vẽ đường thẳng vuông góc với MC tại E và cắt đường thẳng BA tại F. C/m FC là tiếp tuyến của đường tròn (O)
a: Xét tứ giác MAOB có
\(\widehat{OAM}+\widehat{OBM}=180^0\)
Do đó: MAOB là tứ giác nội tiếp
Đúng 0
Bình luận (0)
a) Ta có
MAMA là tiếp tuyến của đường tròn (gt)
OEOI=OMOFOEOI=OMOF (tỉ số đồng dạng)
OCOE=OFOCOCOE=OFOC
⇒⇒ ΔOCF∼ΔOEC∆OCF∼∆OEC (c.g.c)(c.g.c)
⇒⇒ ˆOFC=ˆOCE=90°OFC^=OCE^=90°
⇒⇒ OC⊥CFOC⊥CF tại C
⇒⇒ FCFC là tiếp tuyến của đường tròn
(ĐPCM)
Đúng 1
Bình luận (0)
Từ một điểm M nằm ngoài đường tròn (O) vẽ hai tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Vẽ AH ⊥ MB, BK ⊥ MA (H∈MB,K∈MA). Gọi C là giao điểm của AH và BK. Chứng minh rằng:
b) Ba điểm M, O, C thẳng hàngb) Do AOBC là hình thoi nên AB ⊥ CO
Lại có MA và MB là 2 tiếp tuyến cắt nhau của (O) nên AB ⊥ MO
⇒ M,C,O thẳng hàng.
Đúng 0
Bình luận (0)
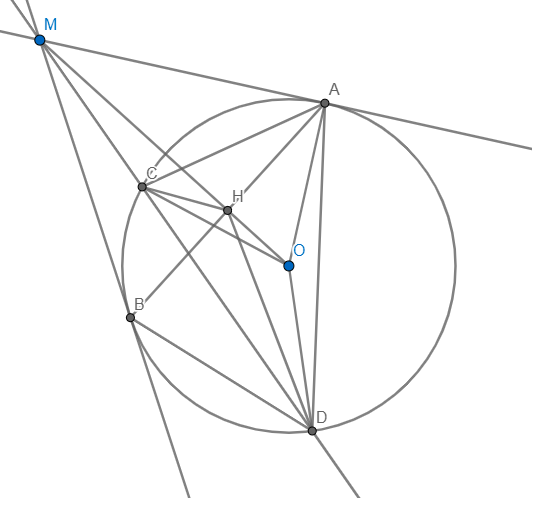
Từ điểm M nằm ngoài đường tròn (O,R) vẽ 2 tiếp tuyến MA và MB và cắt tuyến MCD với (O). Gọi H là giao điểm của OM và AB b. CM: AC.BD = DC.BH
ACBD nội tiếp \(\Rightarrow\angle ACD=\angle ABD=\angle HBD\)
Xét \(\Delta MAC\) và \(\Delta MDA:\) Ta có: \(\left\{{}\begin{matrix}\angle MAC=\angle MDA\\\angle DMAchung\end{matrix}\right.\)
\(\Rightarrow\Delta MAC\sim\Delta MDA\left(g-g\right)\Rightarrow\dfrac{MA}{MD}=\dfrac{MC}{MA}\Rightarrow MA^2=MC.MD\)
Vì MA,MB là tiếp tuyến \(\Rightarrow\Delta MAB\) cân tại M có MO là phân giác \(\angle AMB\)
\(\Rightarrow MO\bot AB\)
tam giác MAO vuông tại A có AH là đường cao \(\Rightarrow MA^2=MH.MO\)
\(\Rightarrow MH.MO=MC.MD\Rightarrow\dfrac{MH}{MD}=\dfrac{MC}{MO}\)
Xét \(\Delta MHC\) và \(\Delta MDO:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{MH}{MD}=\dfrac{MC}{MO}\\\angle DMOchung\end{matrix}\right.\)
\(\Rightarrow\Delta MHC\sim\Delta MDO\left(c-g-c\right)\Rightarrow\angle MHC=\angle MDO\Rightarrow CHOD\) nội tiếp
Ta có: \(\angle BHD=90-\angle DHO=90-\angle DCO\) (CHOD nội tiếp)
\(=90-\dfrac{180-\angle COD}{2}=90-90+\dfrac{1}{2}\angle COD=\angle CAD\)
Xét \(\Delta BHD\) và \(\Delta CAD:\) Ta có: \(\left\{{}\begin{matrix}\angle CAD=\angle BHD\\\angle ACD=\angle HBD\end{matrix}\right.\)
\(\Rightarrow\Delta BHD\sim\Delta CAD\left(g-g\right)\Rightarrow\dfrac{BH}{CA}=\dfrac{BD}{CD}\Rightarrow BH.CD=BD.CA\)
Đúng 1
Bình luận (1)

















