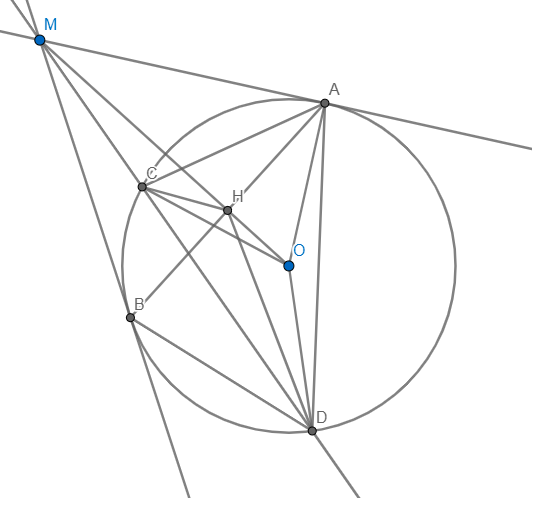
ACBD nội tiếp \(\Rightarrow\angle ACD=\angle ABD=\angle HBD\)
Xét \(\Delta MAC\) và \(\Delta MDA:\) Ta có: \(\left\{{}\begin{matrix}\angle MAC=\angle MDA\\\angle DMAchung\end{matrix}\right.\)
\(\Rightarrow\Delta MAC\sim\Delta MDA\left(g-g\right)\Rightarrow\dfrac{MA}{MD}=\dfrac{MC}{MA}\Rightarrow MA^2=MC.MD\)
Vì MA,MB là tiếp tuyến \(\Rightarrow\Delta MAB\) cân tại M có MO là phân giác \(\angle AMB\)
\(\Rightarrow MO\bot AB\)
tam giác MAO vuông tại A có AH là đường cao \(\Rightarrow MA^2=MH.MO\)
\(\Rightarrow MH.MO=MC.MD\Rightarrow\dfrac{MH}{MD}=\dfrac{MC}{MO}\)
Xét \(\Delta MHC\) và \(\Delta MDO:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{MH}{MD}=\dfrac{MC}{MO}\\\angle DMOchung\end{matrix}\right.\)
\(\Rightarrow\Delta MHC\sim\Delta MDO\left(c-g-c\right)\Rightarrow\angle MHC=\angle MDO\Rightarrow CHOD\) nội tiếp
Ta có: \(\angle BHD=90-\angle DHO=90-\angle DCO\) (CHOD nội tiếp)
\(=90-\dfrac{180-\angle COD}{2}=90-90+\dfrac{1}{2}\angle COD=\angle CAD\)
Xét \(\Delta BHD\) và \(\Delta CAD:\) Ta có: \(\left\{{}\begin{matrix}\angle CAD=\angle BHD\\\angle ACD=\angle HBD\end{matrix}\right.\)
\(\Rightarrow\Delta BHD\sim\Delta CAD\left(g-g\right)\Rightarrow\dfrac{BH}{CA}=\dfrac{BD}{CD}\Rightarrow BH.CD=BD.CA\)