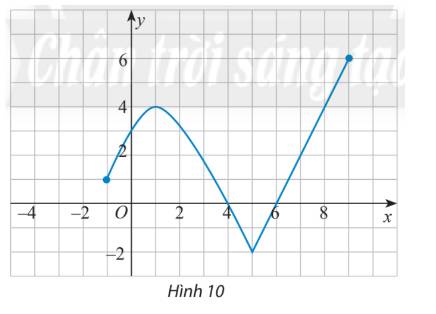
Tìm tập xác định, tập giá trị của hàm số có đồ thị như Hình 10.
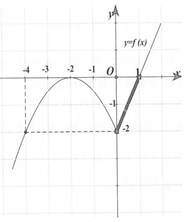
Cho hàm số y=f(x) có đạo hàm xác định trên tập ℝ / 0 và đồ thị hàm số y=f(x) như hình vẽ bên dưới. Có bao nhiêu giá trị nguyên của tham số m để phương trình f cos 2 x = m có nghiệm?
A. Không tồn tại m
B. 1
C. 2
D. 3
Cho hàm số y=f(x) có đạo hàm xác định trên tập R / - 1 và đồ thị hàm số y=f(x) như hình vẽ. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị nhỏ nhất của hàm số y=f(sin2x) trên 0 ; π 2 . Tính P=m.M
A. P=0
B. P=8
C. P=12
D. P=4
Cho hàm số y=f(x) có đạo hàm xác định trên tập r/{0} và đồ thị hàm số y=f(x) như hình vẽ bên dưới.
Có bao nhiêu giá trị nguyên của tham số m để phương trình
f
(
cos
2
x
)
=
m
có nghiệm?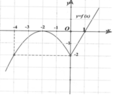
![]()
![]()
![]()
![]()
Cho hàm số y=f(x) có đồ thị như hình vẽ.
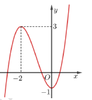
Tìm tập hợp tất cả các giá trị của m để đồ thị hàm số y = f x + m có 5 điểm cực trị.
A. m < 2.
B. m > 2.
C. m > − 2.
D. m < − 2.
Đáp án D
Dựa vào đồ thị hàm số, dễ thấy hàm số f x = x 3 + 3 x 2 − 1
Xét hàm số f x + m = x + m 3 + 3 x + m − 1 với x ∈ ℝ
Chú ý : Cực trị là điểm làm y' đổi dấu và f x = x = x 2 ⇒ f ' x = 2 x 2 x 2 = x x
Do đó f x + m = 3 x + m x + m + 2 . x x .
Khi đó y = f x + m có 5 điểm cực trị x + m = 0 x + m + 2 = 0 có 4 nghiệm phân biệt x = − m x = − 2 − m có 4 nghiệm − m > 0 − 2 − m > 0 ⇔ m < − 2
Cách 2: Đồ thị hàm số y = f x + m được suy ra từ
y = f x → y = f x + m → y = f x + m .
Đồ thị hàm số muốn có 5 điểm cực trị khi ở bước thứ 1ta dịch chuyển đồ thị sang phải nhiều hơn 2 đơn vị m < − 2
Cho hàm số y=2x. Khẳng định nào sau đây là sai?
A. Tập xác định của hàm số là R.
B. Tập giá trị của hàm số là (0;+∞).
C. Đồ thị của hàm số cắt trục Ox tại đúng một điểm.
D. Hàm số đồng biến trên tập xác định của nó.
Đồ thị này cắt trục Ox tại rất nhiều điểm chứ không phải chỉ có 1 điểm
=>Chọn C
Tìm các giá trị thực của tham số m để đồ thị hàm số y = m x + 2 2 x + m đồng biến trên từng khoảng thuộc tập xác định.
A. m ≥ 2 .
B. m > 2 .
C. ∀ m ∈ ℝ .
D. m < 2 .
Đáp án B
Điều kiện: x ≠ − m 2 .
y ' = m 2 − 4 2 x + m 2 ;
Hàm số đồng biến trên từng khoảng thuộc tập xác định
⇔ y ' > 0, ∀ x ≠ − m 2 ⇔ m 2 − 4 > 0, ∀ x ≠ − m 2 ⇔ m > 2.
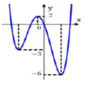
Cho hàm số y = f ( x ) xác định và liên tục trên ℝ , có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = f ( x ) trên đoạn - 2 ; 2
 .
.
A. m = -5, M = 0
B. m = -5, M = -1
C. m = -1, M = 0
D. m = -2, M = 2
Nhận thấy trên đoạn [-2;2]
● Đồ thị hàm số có điểm thấp nhất có tọa độ (-2;-5) và (1;-5)
=> giá trị nhỏ nhất của hàm số này trên đoạn [-2;2] bằng - 5
● Đồ thị hàm số có điểm cao nhất có tọa độ (-1;1) và (-2;1)
=> giá trị lớn nhất của hàm số này trên đoạn [-2;2] bằng -1.
Chọn B.
Cho hàm số y = f (x) có đồ thị như hình bên. Gọi S là tập tất cả các giá trị nguyên dương của tham số m để hàm số y = f x - 2018 + m có 5 điểm cực trị. Tổng tất cả các giá trị của tập S bằng
A. 9
B. 7
C. 12
D. 18
Tìm tập xác định, tập giá trị và vẽ đồ thị hàm số:
\(f(x) = \left\{ \begin{array}{l} - 1\quad \quad x < 0\\1\;\quad \quad \;{\kern 1pt} x > 0\end{array} \right.\quad \)
Tham khảo:
+) Dễ thấy: hàm số được xác định với mọi \(x > 0\) và \(x < 0\).
Do đó tập xác định của hàm số là \(D = \mathbb{R}{\rm{\backslash }}\{ 0\} \)
+) Với \(x \in D\):
+ Nếu \(x > 0\) thì \(f(x) = 1\)
+ Nếu \(x < 0\) thì \(f(x) = - 1\)
Vậy tập giá trị của hàm số là \(T = \{ - 1;1\} \)
+) Vẽ đồ thị hàm số:
Với \(x \in ( - \infty ;0)\) đồ thị hàm số là đường thẳng \(y = - 1\)
Với \(x \in (0; + \infty )\) đồ thị hàm số là đường thẳng \(y = 1\)
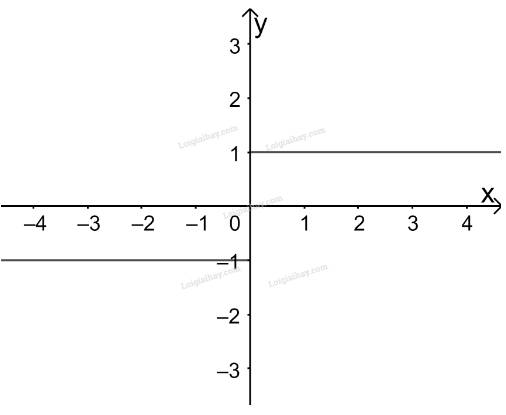
Ta được đồ thị hàm số như hình trên.