Từ đồ thị, ta có:
Đồ thị hàm số xác định (liền mạch) từ \(x = - 1\) đến \(x = 9\), do đó tập xác định của hàm số là \(D = [ - 1;9].\)
Tập giá trị \(T = \{ y|x \in [ - 1;9]\} \), vậy \(T = [ - 2;6]\)
Từ đồ thị, ta có:
Đồ thị hàm số xác định (liền mạch) từ \(x = - 1\) đến \(x = 9\), do đó tập xác định của hàm số là \(D = [ - 1;9].\)
Tập giá trị \(T = \{ y|x \in [ - 1;9]\} \), vậy \(T = [ - 2;6]\)
Tìm tập xác định, tập giá trị và vẽ đồ thị hàm số:
\(f(x) = \left\{ \begin{array}{l} - 1\quad \quad x < 0\\1\;\quad \quad \;{\kern 1pt} x > 0\end{array} \right.\quad \)
Một thiết bị đã ghi lại vận tốc v (mét/giây) ở thời điểm t (giây) của một vật chuyển động như trong bảng sau:
t (giây) | 0,5 | 1 | 1,2 | 1,8 | 2,5 |
v (mét/giây) | 1,5 | 3 | 0 | 5,4 | 7,5 |
Vì sao bảng này biểu thị một hàm số? Tìm tập xác định của hàm số này.
Ở góc của miếng đất hình chữ nhật, người ta làm một bồn hoa có dạng một phần tư hình tròn với bán kính r (Hình 2). Bán kính bồn hoa có kích thước từ 0,5 m đến 3 m.

a) Viết công thức của hàm số biểu thị diện tích bồn hoa theo bán kính r và tìm tập xác định của hàm số này.
b) Bán kính bồn hoa bằng bao nhiêu thì nó có diện tích là \(0,5\pi \;{m^2}?\)
Tìm tập xác định của các hàm số sau:
a) \(f(x) = \sqrt { - 5x + 3} \)
b) \(f(x) = 2 + \frac{1}{{x + 3}}\)
Tìm tập xác định của các hàm số sau:
a) \(f(x) = \sqrt {2x + 7} \)
b) \(f(x) = \frac{{x + 4}}{{{x^2} - 3x + 2}}\)
Xét hàm số \(y = f(x)\) cho bởi bảng sau:
\(x\) | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
\(f(x)\) | 8 | 3 | 0 | -1 | 0 | 3 | 8 |
a) Tìm tập xác định D của hàm số trên.
b) Trong mặt phẳng tọa độ Oxy, vẽ tất cả các điểm có tọa độ (x; y) với \(x \in D\) và \(y = f(x).\)
a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:
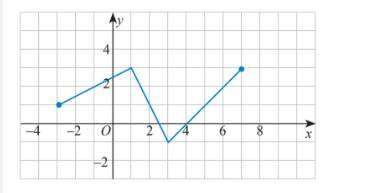
b) Xét tính đồng biến, nghịch biến của hàm số \(y = f(x) = 5{x^2}\) trên khoảng (2; 5).
Vẽ đồ thị hàm số \(f\left( x \right) = \left| x \right|\) biết rằng hàm số này còn được viết như sau:
\(f(x) = \left\{ \begin{array}{l}x\quad \quad (x \ge 0)\\ - x\quad \;\;(x < 0)\end{array} \right.\)
Vẽ đồ thị hàm số \(f(x) = 3x + 8\).