Do \(\left( { - 2\pi ; - \pi } \right) = \left( { - 2\pi ;\pi  - 2\pi } \right)\) nên hàm số \(y = \cos x\) nghịch biến trên khoảng \(\left( { - 2\pi ; - \pi } \right)\)

Trên \(\left(-\dfrac{\pi}{2}+k.2\pi;\dfrac{\pi}{2}+k.2\pi\right)\) chọn 2 giá trị của x (x₁ và x₂) sao cho x₁ > x₂

Xét f(x₁) - f(x₂) = sinx₁ - sinx₂

 = 2cos\(\dfrac{x_1+x_2}{2}\) . sin \(\dfrac{x_1-x_2}{2}\)

Do \(\dfrac{x_1+x_2}{2}\in\left(0;\dfrac{\pi}{2}\right)\)

⇒ cos\(\dfrac{x_1+x_2}{2}\) > 0 

Mà \(sin\dfrac{x_1-x_2}{2}\) > 0 

nên f(x₁) - f(x₂) > 0 

Vậy đồng biến

Nghịch biến tương tự

Hàm số nghịch biến trên khoảng \(\left( {\pi ;2\pi } \right)\) là:\(y = \cos x\)

Chọn B

\(\dfrac{\sqrt{3}}{2}< 1;\dfrac{\sqrt[3]{26}}{3}< 1;\pi>1;\dfrac{\sqrt{15}}{4}< 1\)

Hàm số đồng biến là: \(log_{\pi}x\)

Hàm số nghịch biến là: \(\left(\dfrac{\sqrt{3}}{2}\right)^x;\left(\dfrac{\sqrt[3]{26}}{3}\right)^x;log_{\dfrac{\sqrt{15}}{4}}x\)

Vẽ đồ thị \(y = 3x + 1;y =  - 2{x^2}\)

a) Trên \(\mathbb{R}\), đồ thị \(y = 3x + 1\) đi lên từ trái sang phải, như vậy hàm số \(y = 3x + 1\) đồng biến trên \(\mathbb{R}\)

b) Trên khoảng \(\left( { - \infty ;0} \right)\), đồ thị \(y =  - 2{x^2}\)đi lên từ trái sang phải với mọi \(x \in \left( { - \infty ;0} \right)\) , như vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)

Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị \(y =  - 2{x^2}\)đi xuống từ trái sang phải với mọi \(x \in \left( {0; + \infty } \right)\) , như vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)

y=sin x đồng biến trên \(\left(-\dfrac{\Omega}{2}+k2\Omega;\dfrac{\Omega}{2}+k2\Omega\right)\)

=>Hàm số y=sin x không thể đồng biến trên cả khoảng \(\left(0;\dfrac{5}{6}\Omega\right)\) được

=>Loại A

\(y=cosx\) đồng biến trên khoảng \(\left(-\Omega+k2\Omega;k2\Omega\right)\)

=>Hàm số y=cosx cũng không thể đồng biến trên khoảng \(\left(0;\dfrac{5}{6}\Omega\right)\)

=>Loại B

\(x\in\left(0;\dfrac{5}{6}\Omega\right)\)

=>\(x+\dfrac{\Omega}{3}\in\left(\dfrac{\Omega}{3};\dfrac{4}{3}\Omega\right)\)

=>\(y=sin\left(x+\dfrac{\Omega}{3}\right)\in\left[-\dfrac{\sqrt{3}}{2};\dfrac{\sqrt{3}}{2}\right]\)

=>Khi x tăng thì y chưa chắc tăng

=>Loại D

=>Chọn C 

a)     y = sinx

-        Khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right)\)

+ Vẽ đồ thị hàm số:

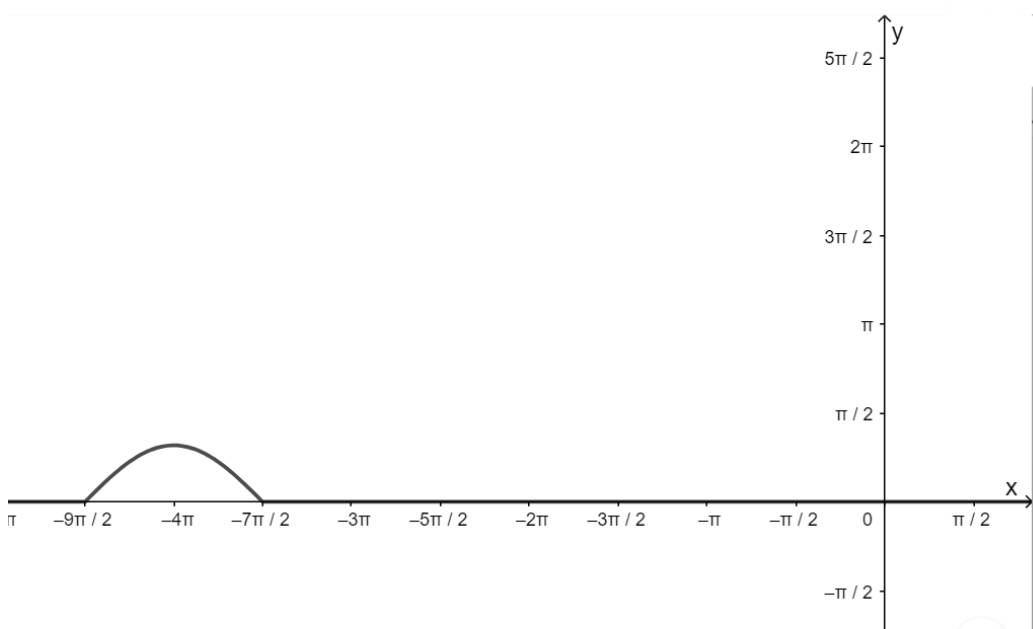
+ Đồng biến trên khoảng \(\left( { - \frac{{9\pi }}{2}; - 4\pi } \right)\)

+ Nghịch biến trên khoảng; \(\left( { - 4\pi ; - \frac{{7\pi }}{2}} \right)\)

-        Khoảng \(\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)

+ Vẽ đồ thị hàm số:

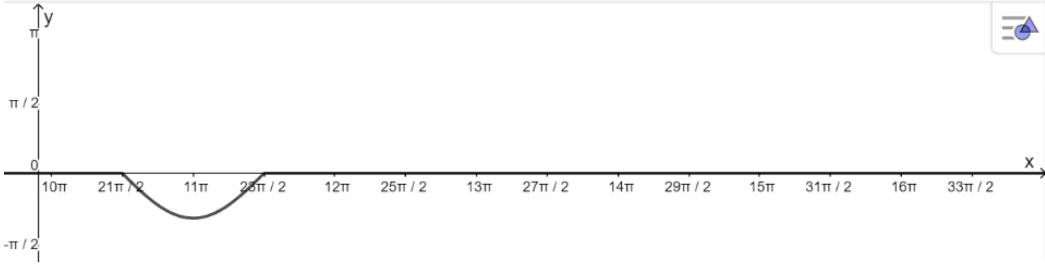
+ Đồng biến trên khoảng: \(\left( {11\pi ;\frac{{23\pi }}{2}} \right)\)

+ Nghịch biến trên khoảng: \(\left( {\frac{{21\pi }}{2};11\pi } \right)\)