Một chiếc hộp đựng 7 tấm thẻ như nhau được ghi số 2;3;4;5;6;7;8. Rút ngẫu nhiên một tấm thẻ trong hộp. Tìm xác suất để rút được tấm thẻ:
a) Ghi số nhỏ hơn 10
b) Ghi số 1
c) Ghi số 8
Một hộp kín đựng 3 chiếc thẻ có hình dạng giống nhau, ghi các số 2, 7, 4. Bạn Khoa rút ra ngẫu nhiên một chiếc thẻ. Hỏi có những khả năng nào về số ghi trên thẻ được lấy ra?
Khả năng 1: Bạn Khoa rút được thẻ số 2
Khả năng 2: Bạn Khoa rút được thẻ số 4
Khả năng 3: Bạn Khoa rút được thẻ số 7
Trong 3 thẻ 2, 7, 4 thì bạn Khoa sẽ có 3 trường hợp
- Trường hợp 1:
Rút ra thẻ số 2: tỉ lệ 33,3%
- Trường hợp 2:
Rút ra thẻ số 7: tỉ lệ 33,3%
- Trường hợp 3
Rút ra thẻ số 4: tỉ lệ 33,3%
Trong một hộp kín đựng 100 tấm thẻ như nhau được đánh số từ 1 tới 100. Lấy ngẫu nhiên ba tấm thẻ trong hộp. Tính xác suất lấy được 3 tấm thẻ mà số ghi trên 3 tấm thẻ đó lập thành :
a) Một cấp số cộng ?
b) Một cấp số nhân ?
Ý tưởng khá đơn giản:
a/ Cấp số cộng thì \(a+c=2b\) nên a;c cùng tính chẵn lẻ, vậy chỉ cần tìm số cặp cùng tính chẵn lẻ
b/ Cấp số nhân thì \(a.q^2=c\), do đó chỉ cần tìm số bội số phân biệt của các số chính phương không lớn hơn 100
Một hộp đựng 15 tấm thẻ cùng loại được đánh số từ 1 đến 15. Rút ngẫu nhiên một tấm thẻ và quan sát số ghi trên thẻ. Gọi A là biến cố “Số ghi trên tấm thẻ nhỏ hơn 7”; B là biến cố “Số ghi trên tấm thẻ là số nguyên tố”.
a) Mô tả không gian mẫu.
b) Mỗi biến cố \(A \cup B\) và AB là tập con nào của không gian mẫu?
a) Không gian mẫu là các tấm thẻ được đánh số nên nó gồm 15 phần tử, ký hiệu \(\Omega = \left\{ {1;2;3;...;15} \right\}\)
b) A là biến cố “Số ghi trên tấm thẻ nhỏ hơn 7” nên \(A = \left\{ {1;2;3;4;5;6} \right\}\)
B là biến cố “Số ghi trên tấm thẻ là số nguyên tố” nên \(B = \left\{ {2;3;5;7;11;13} \right\}\)
\(A \cup B = \left\{ {1;2;3;4;5;6;7;11;13} \right\}\)
\(AB = \left\{ {2;3;5} \right\}\)
Một hộp đựng 26 tấm thẻ được đánh số từ 1 đến 26. Bạn Hải rút ngẫu nghiên cùng một lúc ba tấm thẻ. Hỏi có bao nhiêu cách rút sao cho bất kỳ hai trong ba tấm thẻ lấy ra đó có hai số tương ứng ghi trên hai tấm thẻ luôn hơn kém nhau ít nhất 2 đơn vị ?
A. 1768.
B. 1771.
C. 1350.
D. 2024.
Một hộp đựng 26 tấm thẻ được đánh số từ 1 đến 26. Bạn Hải rút ngẫu nhiên cùng một lúc ba tấm thẻ. Hỏi có bao nhiêu cách rút sao cho bất kỳ hai trong ba tấm thẻ lấy ra đó có hai số tương ứng ghi trên hai tấm thẻ luôn hơn kém nhau ít nhất 2 đơn vị?
A. 1768
B. 1771
C. 1350
D. 2024
Yêu cầu bài toán thỏa mãn khi ta rút được 3 thẻ sao cho trong đó không có 2 thẻ nào là số tự nhiên liên tiếp
Số cách rút được 3 thẻ bất kì là C 26 3
Số cách rút được 3 thẻ có đúng 2 số tự nhiên liên tiếp:
Chọn 2 số tự nhiên liên tiếp: {1;2}{2;3}…{25;26}
TH1: Chọn 2 thẻ là {1;2} hoặc{25;26}: có 2 cách
Thẻ còn lại không được là 3 (hoặc 24): 26 -3 =23 (cách)
→ 2.23 =46 (cách)
TH2: Chọn 2 thẻ là: {2;3},{3;3},…{24;25}: 23 cách
Thẻ còn lại chỉ có: 26 -4 =22 (cách) →có 23.22 =506 (cách)
Số cách rút 3 thẻ trong đó có 3 số tự nhiên liên tiếp:
{1;2;3}{2;3;4}…{24;25;26}: 24 cách
Vậy có: C 26 3 - 46 - 506 - 24 = 2024 .
Chọn đáp án D.
Một hộp đựng 10 tấm thẻ phân biệt gồm 6 tấm thẻ ghi số 1 và 4 tấm thẻ ghi số 0. Một trò chơi được thực hiện bằng cách rút ngẫu nhiên một thẻ từ hộp rồi hoàn lại. Sau một số lần rút, trò chơi sẽ kết thúc khi có đúng 3 lần rút được thẻ ghi số 1 hoặc hoặc đúng 3 lần thẻ ghi số 0. Tính xác suất để trò chơi kết thúc khi có đúng 3 lần rút được thẻ ghi số 1.
A. 0,9072
B. 0,33696
C. 0,456
D. 0,68256
Trong một chiếc hộp có 15 tấm thẻ giống nhau được đánh số 10; 11;...; 24. Rút ngẫu nhiên một tấm thẻ từ trong hộp. Tính xác suất của các biến cố sau:
a) A: "Rút được tấm thẻ ghi số lẻ"
b) B: "Rút được tấm thẻ ghi số nguyên tố"
Có 15 kết quả có thể xảy ra. Do 15 tấm thẻ giống nhau nên 15 kết quả có thể này là đồng khả năng
a) Có 11; 13; 15; 17; 19; 21; 23 là số lẻ => Có 7 kết quả thận lợi cho biến cố A. Do đó xác suất của biến cố A là \(P(A) = \frac{7}{{15}}\)
b) Có 11; 13; 17; 19; 23 là số nguyên tố => Có 5 kết quả thuận lợi cho biến cố B. Do đó xác suất của biến cố B là \(P(B) = \frac{5}{{15}} = \frac{1}{3}\)
. Một hộp đựng 15 tấm thẻ được đánh số từ 1 đến 15 . Chọn ngẫu nhiên 5 tấm thẻ. Tính xác suất để
tổng số ghi trên 5 tấm thẻ ấy là một số lẻ.
Không gian mẫu: \(C_{15}^5\)
Tổng số 5 tấm thẻ là lẻ khi số số thẻ lẻ là 1 số lẻ, gồm các trường hợp: (1 thẻ lẻ, 4 thẻ chẵn), (3 thẻ lẻ, 2 thẻ chẵn), (5 thẻ đều lẻ)
Trong 15 tấm thẻ có 7 thẻ chẵn và 8 thẻ lẻ
\(\Rightarrow\) Số biến cố thuận lợi: \(C_8^1.C_7^4+C_8^3.C_7^2+C_8^5\)
Xác suất: ...
Một hộp có 10 chiếc thẻ cùng loại , mỗi thẻ được ghi một trong các số 1, 2, 3,..., 10; hai thẻ khác nhau thì ghi hai số khác nhau.
Rút ngẫu nhiên một chiếc thẻ từ trong hộp, ghi lại số của thẻ rút được và bỏ lại thẻ đó vào hộp. Sau 25 rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
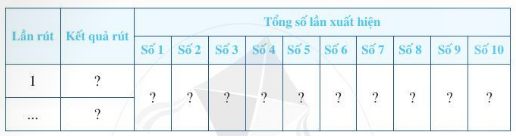
Tính xác suất thực nghiệm:
a) Xuất hiện số 1;
b) Xuất hiện số 5;
c) Xuất hiện số 10.