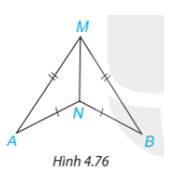
Trong Hình 4.76, có AM = BM, AN = BN. Chứng minh rằng\(\widehat {MAN} = \widehat {MBN}\).
Những câu hỏi liên quan
Trong Hình 4.78, ta có AN = BM,\(\widehat {BAN} = \widehat {ABM}\). Chứng minh rằng\(\widehat {BAM} = \widehat {ABN}\).
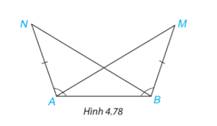
Xét \(\Delta ANB \) và \(\Delta BMA\) có:
AN=BM (gt)
\(\widehat {BAN} = \widehat {ABM}\) (gt)
AB chung
=>\(\Delta ANB = \Delta BMA\)(c.g.c)
=> \(\widehat{ABN} = \widehat{BAM}\) (2 góc tương ứng)
Đúng 0
Bình luận (0)
Trong Hình 4.77, có AO = BO,\(\widehat {OAM} = \widehat {OBN}\). Chứng minh rằng AM = BN.
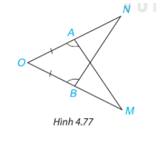
Xét 2 tam giác OAM và OBN có:
\(\widehat {OAM} = \widehat {OBN}\) (gt)
AO=BO (gt)
\(\widehat{O}\) chung
=>\(\Delta OAM = \Delta OBN\)(g.c.g)
=>AM=BN (2 cạnh tương ứng)
Đúng 0
Bình luận (0)
trong tam giác ABC có \(\widehat{B}=3\widehat{A}\). lấy 2 điểm M,N trên AC sao cho \(\widehat{CBM}=\widehat{MBN}=\widehat{NBA}\). lấy E thuộc BC, F là giao điểm của AE với BN, K là giao điểm của NE với BM. chứng minh rằng FK song song với AC.
trong tam giác ABC có \(\widehat{B}=3\widehat{A}\). lấy 2 điểm M,N trên AC sao cho \(\widehat{CBM}=\widehat{MBn}=\widehat{NBA}\). lấy E thuộc BC, F là giao điểm của AE với BN, K là giao điểm của NE với BM. chứng minh rằng FK song song với AC
Cho tam giác ABC sao cho tồn tại các điểm M,N lần lượt trên 2 cạnh AB,BC sao cho 2\(\frac{BM}{AN}\)=\(\frac{BN}{CN}\)và\(\widehat{BNM}\)=\(\widehat{ANC}\).Gọi P là trung điểm AM,Q là giao điểm AN với CP.
a,Chứng minh MN // CP
b,Chứng minh tam giác AQC cân tại Q
c,Chứng minh tam giác ABC vuông tại C
Cho Hình 65 có AM = BN, \(\widehat A = \widehat B\). Chứng minh: OA = OB, OM = ON.
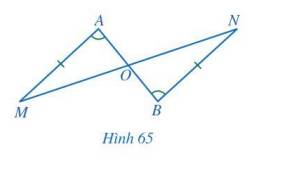
Ta có: \(\widehat A = \widehat B\)
Mà 2 góc này ở vị trí so le trong nên AM // BN
\(\Rightarrow \widehat M = \widehat N\)(2 góc so le trong).
Xét hai tam giác AOM và BON có: \(\widehat A = \widehat B\), AM = BN, \(\widehat M = \widehat N\).
Vậy \(\Delta AOM = \Delta BON\) (g.c.g)
Do đó OA = OB, OM = ON. (2 cạnh tương ứng).
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A . Trên cạnh đáy BC lấy điểm M và N sao cho BM = MN = NC . Chứng minh rằng \(\widehat{MAN}>\widehat{NAC}\)
Cho tam giác ABC cân tại A, trên cạnh BC lần lượt lấy hai điểm M và N sao cho BM = MN = NC. Gọi H là trung điểm của BC.
a) Chứng minh AM = AN và AH vuông góc với BC.
b) Tính độ dài đoạn thẳng AM khi AB = 5cm, BC = 6cm.
c) Chứng minh: \(\widehat{MAN}>\widehat{BAM}=\widehat{CAN}\)
a: Xet ΔAMB và ΔANC có
AB=AC
\(\widehat{B}=\widehat{C}\)
BM=CN
Do đó: ΔAMB=ΔANC
Suy ra: AM=AN
Ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là đường cao
b: BC=6cm nên BH=CH=3cm
=>AH=4(cm)
BM=BC/3=2(cm)
=>MH=1(cm)
\(AM=\sqrt{1^2+4^2}=\sqrt{17}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có \(\widehat{ABC}\)= \(50^0\),\(\widehat{BAC}=70^0\).Phân giác trong \(\widehat{ACB}\) cắt AB tại M.Trên MC lấy điểm N sao cho \(\widehat{MBN}=40^0\).Chứng minh BN=MC