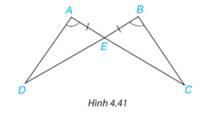
Chứng minh rằng hai tam giác ADE và BCE trong Hình 4.41 bằng nhau.
Cho hình thang ABCD có 2 đáy AB , CD biết CD gấp 3 lần AB . Hai đường chéo AC vá BD cắt nhau tại E . Chứng minh S tam giác ADE = S tam giác BCE và tính tỉ số EA trên EC
Cho tam giác \(ADE\) và tam giác \(ACF\) có các kích thước như trong Hình 8. Chứng minh rằng \(\Delta ADE\backsim\Delta ACF\).
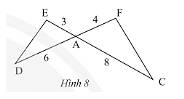
Ta có: \(\frac{{AE}}{{AF}} = \frac{3}{4};\frac{{AD}}{{AC}} = \frac{6}{8} = \frac{3}{4}\);
Xét \(\Delta ADE\) và \(\Delta ACF\) có:
\(\frac{{AE}}{{AF}} = \frac{{AD}}{{AC}} = \frac{3}{4}\)
\(\widehat {EAD} = \widehat {FAC}\) (hai góc đối đỉnh)
Do đó, \(\Delta ADE\backsim\Delta ACF\)(c.g.c)
Cho hình chữ nhật ABCD có AB=8cm, BC=6cm và hai đường chéo cắt nhau tại O. Qua B kẻ đường thẳng a vuông góc với BD, a cắt DC tại E.
a) Chứng minh tam giác BCE~tam giác DBE
b) Kẻ đường cao CH của tam giác BCE. Chứng minh BC^2=CH.BD
c) Tính tỉ số diện tích tam giác CEH và diện tích của tam giác DBE
d) Chứng minh 3 đường OE, BC, DH đồng quy
a: Xét ΔBCE vuông tại C và ΔDBE vuông tại B có
góc E chung
=>ΔBCE đồng dạng với ΔDBE
b: Xét ΔCBD vuông tại C và ΔHCB vuông tại H có
góc CBD=góc HCB
=>ΔCBD đồng dạng với ΔHCB
=>CB/HC=BD/CB
=>BC^2=HC*BD
c: CE=6^2/8=4,5cm
CH//DB
=>ΔEHC đồng dạng với ΔEBD
=>S EHC/S EBD=(EC/ED)^2=(4,5/12,5)^2=81/625
Cho tam giác ABC vuông tại A và AB <AC. Tia phân giác của góc ABC cắt cạnh AC tại D. Kẻ DE vuông góc với BC (điểm E thuộc BC).
a) Chứng minh rằng: Hai tam giác ABD và EBD bằng nhau;
b) Giải thích vì sao tam giác ADE là tam giác cân?
c) Chứng minh: 2.AD>AE;
d) Tia ED cắt tia BA tại F. Chứng minh: BD vuông góc với CF
a) Xét ABD và EBD có
BD cạnh chung
BAD=BED(=90)
ABD=EBD(vì BD là tia phân giác của B)
b ko biet
c) vì theo ý b) ADE là tam giác cân tại D nên theo py-ta-go AD+DE=AE
Nên AE>AD
(sai đầu bài rồi)
b)Vì theo ý a) BAD=BED và BD là tia phân giác của B. Nên ADE là tam giác cân
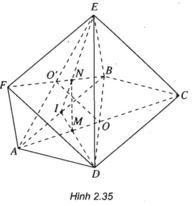
Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt .Gọi O là giao điểm của AC và BD, O’ là giao điểm của AE và BF.
a) Chứng minh rằng OO’ song song với hai mặt phẳng (ADF) và (BCE)
b) Gọi M và N lần lượt là trọng tâm của các tam giác ABDvà ABE. Chứng minh rằng .
a) Ta có : OO′ // DF ( đường trung bình của tam giác BDF).
Vì DF ⊂ (ADF) ⇒ OO′ // (ADF).
Tương tự OO’ // EC (đường trung bình của tam giác AEC).
Vì EC ⊂ (BCE) nên OO′ // (BCE).
b) Gọi I là trung điểm AB;
Vì M là trọng tâm của tam giác ABD nên M ∈ DI
Vì N là trọng tâm của tam giác ABE nên N ∈ EI
Ta có :
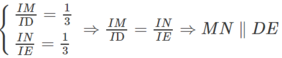
Mà
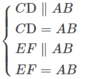
Nên CD // EF và CD = EF, suy ra tứ giác CDFE là hình bình hành.
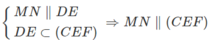
hình thang ABCD ( AB // CD ) có E thuộc đáy CD. Biết rằng các tam giác ADE , ABE, CBE có chu vi bằng nhau .. chứng minh rằng CD= 2AB
Hình thang ABCD (AB//CD) có CD=2AB. Gọi E là trung điểm của DC. Chứng minh rằng ba tam giác ADE, ABE và BEC đồng dạng với nhau từng đôi một (Chú ý viết đỉnh của hai tam giác đồng dạng theo thứ tự tương ứng với nhau)
Bài 19. Dựng ra ngoài tứ giác ABCD các tam giác đều BCE, ADF, dựng vào trong tứ giác ABCD các tam giác đều ABG, CDH. Chứng minh rằng EF và GH cắt nhau tại trung điểm mỗi đoạn.
Cho hình chữ nhật ABCD, có AB=8cm, BC=6cm, và hai đường chéo cắt nhau tại O, qua B kẻ đường thẳng a vuông góc với BD, a cắt DC tại E
a) cm tam giác BCE và tam giác DBE đồng dạng
b) kẻ đường caoCH của tam giác BCE , chứng minh BC2 = CH.BD
c) tính tỉ số diện tích của tam giác CEH và diện tích tam giác DEB
d)chứng minh ba đường OE,BC,DH cắt nhau tại 1 điểm
a)xét tam giác BCE và tam giác DCE có:
\(\widehat{DBE}=\widehat{BCE}=90^o\)
\(\widehat{BEC}:chung\)
nên tam giác BCE ~ tam giác DBE(g-g)
vì \(\Delta BCE\) ~ \(\Delta DBE\)
nên \(\widehat{CBH}=\widehat{BDC}\)
đồng thời: \(\widehat{CHB}=\widehat{DCB}=90^o\)
do đó tam giác BCH ~ DBC (g-g)
\(\Rightarrow\dfrac{BD}{BC}=\dfrac{BC}{CH}\) hay \(BC^2=CH.BD\)