Với số liệu đo đạc được ghi trên Hình 14, hãy tính bề rộng \(CD\) của con kênh.
Với số liệu được ghi trên Hình 21. Hãy tính khoảng cách \(CD\) từ con tàu đến trạm quan trắc đặt tại điểm \(C\).
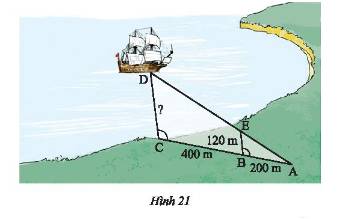
Ta có \(\widehat {ABE} = \widehat {ACD}\), mà hai góc này ở vị trí đồng vị nên \(BE//CD\).
Ta có: \(AC = AB + BC = 200 + 400 = 600m\)
Xét tam giác \(ACD\) có \(BE//CD\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{AB}}{{AC}} = \frac{{BE}}{{CD}} \Rightarrow \frac{{200}}{{600}} = \frac{{120}}{{CD}}\). Do đó, \(CD = \frac{{120.600}}{{200}} = 360\).
Vậy \(CD = 360m\).
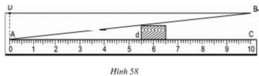
Hình 58 dưới đây mô tả dụng cụ đo bề dày của một số loại sản phẩm. Dụng cụ này gồm thước AC được chia đến 1mm và gắn với một bản kim loại hình tam giác ABD, khoảng cách BC = 10mm.
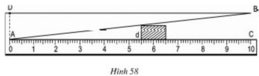
Muốn đo bề dày của vật, ta kẹp vật vào giữa bản kim loại và thước (đáy của vật áp vào bề mặt của thước AC). Khi đó, trên thước AC ta đọc được "bề dày" d của vật (trên hình vẽ ta có có d = 5,5mm).
Hãy chỉ rõ định lí nào của hình học là cơ sở để ghi các vạch trên thước AC (d ≤ 10mm)
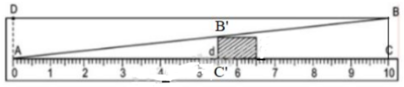
Theo hình vẽ và dựa vào định lí hai tam giác đồng dạng ta có:
ΔABC  ΔAB’C’ (vì B’C’ // BC).
ΔAB’C’ (vì B’C’ // BC).
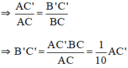
(Vì AC = 10cm, BC = 1cm).
Vậy khi đọc AC’ = 5,5cm thì bề dày của vật B’C’ = 5,5mm.
Dụng cụ trên đã dùng tính chất hai tam giác đồng dạng thì các cạnh tương ứng tỉ lệ.
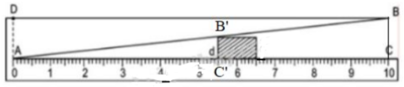
Hình 58 dưới đây mô tả dụng cụ đo bề dày của một số loại sản phẩm. Dụng cụ này gồm thước AC được chia đến 1mm và gắn với một bản kim loại hình tam giác ABD, khoảng cách BC = 10mm.
Muốn đo bề dày của vật, ta kẹp vật vào giữa bản kim loại và thước (đáy của vật áp vào bề mặt của thước AC). Khi đó, trên thước AC ta đọc được "bề dày" d của vật (trên hình vẽ ta có có d = 5,5mm).
Hãy chỉ rõ định lí nào của hình học là cơ sở để ghi các vạch trên thước AC (d ≤ 10mm)
Theo hình vẽ và dựa vào định lí hai tam giác đồng dạng ta có:
ΔABC  ΔAB’C’ (vì B’C’ // BC).
ΔAB’C’ (vì B’C’ // BC).
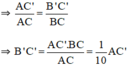
(Vì AC = 10cm, BC = 1cm).
Vậy khi đọc AC’ = 5,5cm thì bề dày của vật B’C’ = 5,5mm.
Dụng cụ trên đã dùng tính chất hai tam giác đồng dạng thì các cạnh tương ứng tỉ lệ.
Một nhà toán học muốn ước lượng chiều rộng của một cái hồ. Ông ta đánh dấu 5 điểm gần hồ và dùng kỹ thuật đo đạc để có được các số liệu như hình vẽ bên (tính theo đơn vị mét). Biết QR song song ST, hỏi chiều rộng của hồ (đoạn PQ) là bao nhiêu mét? Giải thích. (làm tròn đến chữ số thập phân thứ nhất)
Tạo chương trình tính chu vi, diện tích hình chữ nhật với số đo chiều dài, chiều rộng được nhập từ bàn phím. Thực hiện chương trình với bộ dữ liệu dưới đây và ghi kết quả vào vở.

Các số liệu về kênh đào Xuy–ê (Ai Cập) nối Địa Trung Hải và Hồng Hải được cho trong bảng 1 và bảng 2.
Trong bảng 1, các số liệu ở năm 1955 tăng thêm (hay giảm bớt) bao nhiêu so với năm 1869 (năm khánh thành kênh đào)?
Bảng 1
| Kênh đào Xuy–ê | Năm 1869 | Năm 1955 |
| Chiều rộng mặt kênh | 58m | 135m |
| Chiều rộng đáy kênh | 22m | 50m |
| Độ sau của kênh | 6m | 13m |
| Thời gian tàu qua kênh | 48 giờ | 14 giờ |
Bảng 2
| Hành trình | Qua mũi Hảo Vọng | Qua kênh Xuy–ê |
| Luân Đôn – Bom–bay | 17400km | 10100km |
| Mác–xây – Bom-bay | 16000km | 7400km |
| Ô–đét-xa – Bom–bay | 19000km | 6800km |
Trong bảng 1: Số liệu năm 1955 so với năm 1869
Chiều rộng mặt kênh tăng: 135 – 58 = 77 (m)
Chiều rộng đáy kênh tăng: 50 – 22 = 28 (m)
Độ sâu của kênh tăng: 13 – 6 = 7 (m)
Thời gian tàu qua kênh giảm: 48 – 14 =34 (giờ)
Hình 58 dưới đây mô tả dụng cụ đo bề dày của một số sản phẩm. Dụng cụ này gồm thước AC được chia đến 1mm và gắn với một bản kim loại hình tam giác ABD, khoảng cách BC = 10mm
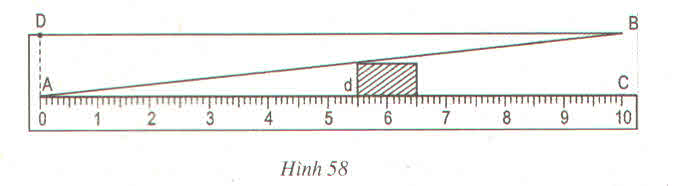
Muốn đo bề dày của vật, ta kẹp vào giữa bản kim loại và thước (đáy của vật áp vào bề mặt của thước AC). Khi đó, trên thước AC ta đọc được "bề dày" d của vật (trên hình vẽ ta có d = 5,5mm)
Hãy chỉ rõ định lí nào của hình học là cơ sở để ghi các vạch trên thước AC (\(\left(d\le10mm\right)\) ?
Theo hình vẽ và dựa vào định lí hai tam giác đồng dạng ta có:
Dụng cụ trên đã dùng tính chất hai tam giác đồng dạng thì các cạnh tương ứng tỉ lệ.
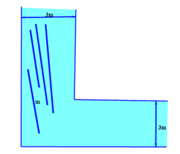
Một kênh dẫn nước theo vuông góc có bề rộng 3,0 m như hình vẽ.
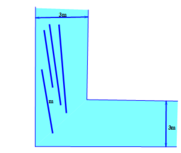
Cho 4 cây luồng (thẳng) có độ dài là 6,2m ; 8,3m ; 8,4m ; 9,0m trôi tự do trên kênh. Hỏi số cây luồng có thể trôi tự do qua góc kênh là bao nhiêu ?
A. 1
B. 4
C. 3
D. 2
Đáp án C
Phương pháp: Phân tích đề bài và tìm giá trị lớn nhất của cây luồng để có thể trôi qua khúc sông.
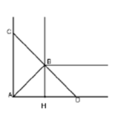
Cách giải:
Để cây luồng có thể trôi qua khúc sông thì độ dài cây luồng không được vượt quá độ dài đoạn thẳng CD với CD là đoạn thẳng đi qua B và vuông góc với AB như hình vẽ.
Xét tam giác vuông ABH ta dễ dàng tính được . A B = 3 2
Tam giác ACD vuông tại A và có AB là phân giác đồng thời là đường cao nên Δ A C D cân tại B
AB là trung tuyến ứng với cạnh huyền.
⇒ A B = 1 2 C D ⇒ C D = 2 A B = 6 2 ≈ 8,48
Vậy trong 4 cây luồng trên chỉ có cây luồng dài 9m không trôi qua được khúc sông.
Một kênh dẫn nước theo vuông góc có bề rộng 3,0 m như hình vẽ. Cho 4 cây luồng (thẳng) có độ dài là 6,2m ; 8,3m ; 8,4m ; 9,0m trôi tự do trên kênh. Hỏi số cây luồng có thể trôi tự do qua góc kênh là bao nhiêu ?
A. 1
B. 4
C. 3
D. 2