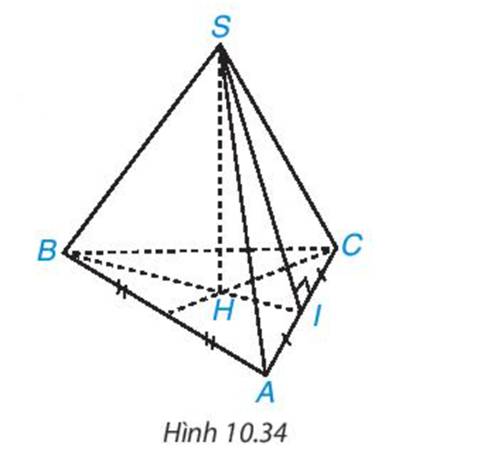
Trung đoạn của hình chóp tam giác đều trong Hình 10.34 là:
A. SB
B. SH
C. SI
D. HI
Dạng 3: Hình chóp tứ giác đều và hình chóp tam giác đều, diện tích và thể tích
Bài 10. Cho một hình chóp tam giác đều có độ dài cạnh đáy là
30
cm và độ dài trung đoạn là
2
dm. Diện tích xung quanh của hình chóp tam giác đều đó là:
A.
900
dm2 B.
90
dm2 C.
900
cm2 D.
90
cm2
Bài 11. Cho hình chóp tứ giác đều có thể tích bằng
3
100cm
và chiều cao của hình chóp dài
12cm.
Độ dài cạnh đáy của hình chóp là:
A. 7cm
B.
6cm
C.
5cm
D.
4cm
10: Chu vi đáy là 30*3=90(cm)
Diện tích xung quanh là \(90\cdot20=1800\left(cm^2\right)\)
=>Không có câu nào đúng
11;
\(V_{chóp}=\dfrac{1}{3}\cdot S_{đáy}\cdot h\)
=>\(\dfrac{1}{3}\cdot12\cdot S_{đáy}=100\)
=>\(S_{đáy}=25\left(cm^2\right)\)
Độ dài cạnh là \(\sqrt{25}=5\left(cm\right)\)
=>Chọn C
Trong các phát biểu sau, phát biểu nào đúng?
Chiều cao của hình chóp tam giác đều là:
A. độ dài đoạn thẳng nối từ đỉnh của hình chóp tới trung điểm của một cạnh đáy
B. chiều cao của mặt đáy
C. độ dài đường trung tuyến của một mặt bên của hình chóp
D. độ dài đoạn thẳng nối từ đỉnh tới trọng tâm của tam giác đáy.
Cho hình chóp S.ABCD với đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên SC= a 15 Tam giác SAD là tam giác đều cạnh 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm của cạnh AD, khoảng cách từ B tới mặt phẳng (SHC) bằng 2 6 a Tính thể tích V của khối chóp S.ABCD?
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCDvới đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên S C = a 15 . Tam giác SAD là tam giác đều cạnh 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm của cạnh AD, khoảng cách từ B tới mặt phẳng (SHC) bằng 2 6 a . Tính thể tích V của khối chóp S,ABCD?
A. V = 8 6 a 3
B. V = 12 6 a 3
C. V = 4 6 a 3
D. V = 24 6 a 3
Đáp án C
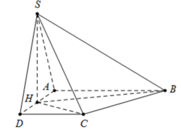
Tam giác SAD đều cạnh 2 a ⇒ S H = a 3 ⇒ H C − 2 a 3 .
Kẻ BK vuông góc H C ⇒ B K ⊥ S H C ⇒ B K − 2 a 6
Diện tích tam giác BHC là S Δ B H C = 1 2 B K . H C = 6 a 2 2
Mà S A B C D = S Δ H A B + S Δ H C D + S Δ H B C = 1 2 S A B C D + S Δ H B C ⇒ S A B C D = 2 x S Δ H B C = 12 a 2 2
V S . A B C D = 1 3 . S H . S Δ H B C = 1 3 . a 3 .12 a 2 2 = 4 6 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên S C = a 15 . Tam giác SAD là tam giác đều cạnh bằng 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm AD, khoảng cách từ B đến mặt phẳng (SHC) bằng 2 a 6 . Tính thể tích V của khối chóp S.ABCD?
A. V = 8 a 3 6 .
B. V = 12 a 3 6 .
C. V = 4 a 3 6 .
D. V = 24 a 3 6 .
Đáp án C.
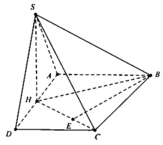
Ta có SAD là tam giác đều nên S H ⊥ A D
Mặt khác S A D ⊥ A B C D ⇒ S H ⊥ A B C D .
Dựng B E ⊥ H C ,
do B E ⊥ S H ⇒ B E ⊥ S H C
Do đó d = B E = 2 a 6 ; S H = a 3 ; A D = 2 a
Do S C = a 15 ⇒ H C = S C 2 − S H 2 = 2 a 3 .
Do S A H B + S C H D = 1 2 a A B + C D = S A B C D 2
suy ra V S . A B C D = 2 V S . H B C = 2 3 . S H . S B C H
= 3 2 a 3 . B E . C H 2 = 4 a 3 6 .
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên SC=a 15 . Tam giác SAD là tam giác đều cạnh bằng 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm AD, khoảng cách từ B đến mặt phẳng (SHC) bằng 2a 6 . Tính thể tích V của khối chóp S.ABCD?
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên SC= a 15 Tam giác SAD là tam giác đều cạnh bằng 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm AD, khoảng cách từ B đến mặt phẳng (SHC) bằng 2 a 6 Tính thể tích V của khối chóp S.ABCD?
![]()
![]()
![]()
![]()
Câu 12: Hình chiếu đứng của hình chóp đều là:
A. Hình vuông B. Hình chữ nhật C. Hình thang D. Hình tam giác cân
Câu 13: Hình chiếu bằng của hình chóp đều (đáy là hình vuông) là:
A. Hình vuông B. Hình chữ nhật C. Hình thang D. Hình tròn
Câu 14: Các hình chiếu đứng, bằng, cạnh của hình nón là:
A. hình tam giác cân và 1 đa giác đều B. 2 hình tam giác cân và 1 hình tròn
C. 2 hình tam giác cân và 1 hình vuông D. 2 hình tam giác cân và 1 hình chữ nhật
Câu 15: Hình trụ được tạo thành khi quay:
A. Hình chữ nhật với nửa hình tròn
B. Hình chữ nhật một vòng quanh một cạnh cố định
C. Hình tam giác vuông một vòng quanh một cạnh góc vuông cố định
D. Nửa hình tròn một vòng quanh một đường kính cố định
Câu 16: Để biểu diễn rõ ràng bộ phận bên trong bị che khuất của vật thể , người ta dùng:
A. Hình chiếu đứng B. Hình chiếu bằng C. Hình cắt D. Hình chiếu cạnh
Câu 17: Hình cắt là hình biểu diễn phần vật thể ở:
A. Trước mặt phẳng cắt B. Sau mặt phẳng cắt
C. Trên mặt phẳng cắt D. Dưới mặt phẳng cắt
Câu 18: Trình tự đọc bản vẽ chi tiết là:
A. Khung tên, kích thước, hình biểu diễn,yêu cầu kĩ thuật,tổng hợp
B. Hình biểu diễn,khung tên,kích thước, yêu cầu kĩ thuật, tổng hợp
C. Khung tên,hình biểu diễn,kích thước, yêu cầu kĩ thuật, tổng hợp
D. Hình biểu diễn,kích thước,khung tên, yêu cầu kĩ thuật, tổng hợp
Câu 19: Kích thước trên bản vẽ kĩ thuật tính theo đơn vị:
A. mm B. cm C. dm D. m
Câu 20: Bản vẽ lắp có thêm nội dung nào mà bản vẽ chi tiết không có?
A. Hình biểu diễn B. Kích thước C. Bảng kê D. Khung tên
Câu 21: Khi đọc bản vẽ chi tiết phải đọc nội dung gì trước?
A. Hình biểu diễn B. Kích thước C. Yêu cầu kĩ thuật D. Khung tên
Câu 22: Trình tự đọc bản vẽ lắp là:
A. Khung tên,bảng kê, hình biểu diễn, kích thước, phân tích chi tiết, tổng hợp
B. Khung tên, hình biểu diễn,bảng kê, kích thước, phân tích chi tiết, tổng hợp
C. Khung tên, hình biểu diễn, bảng kê, phân tích chi tiết, kích hước, tổng hợp
D. Hình biểu diễn, khung tên, bảng kê, phân tích chi tiết, kích thước, tổng hợp
Câu 12: Hình chiếu đứng của hình chóp đều là:
A. Hình vuông B. Hình chữ nhật C. Hình thang D. Hình tam giác cân
Câu 13: Hình chiếu bằng của hình chóp đều (đáy là hình vuông) là:
A. Hình vuông B. Hình chữ nhật C. Hình thang D. Hình tròn
Câu 14: Các hình chiếu đứng, bằng, cạnh của hình nón là:
A. hình tam giác cân và 1 đa giác đều B. 2 hình tam giác cân và 1 hình tròn
C. 2 hình tam giác cân và 1 hình vuông D. 2 hình tam giác cân và 1 hình chữ nhật
Câu 15: Hình trụ được tạo thành khi quay:
A. Hình chữ nhật với nửa hình tròn
B. Hình chữ nhật một vòng quanh một cạnh cố định
C. Hình tam giác vuông một vòng quanh một cạnh góc vuông cố định
D. Nửa hình tròn một vòng quanh một đường kính cố định
Câu 16: Để biểu diễn rõ ràng bộ phận bên trong bị che khuất của vật thể , người ta dùng:
A. Hình chiếu đứng B. Hình chiếu bằng C. Hình cắt D. Hình chiếu cạnh
Câu 17: Hình cắt là hình biểu diễn phần vật thể ở:
A. Trước mặt phẳng cắt B. Sau mặt phẳng cắt
C. Trên mặt phẳng cắt D. Dưới mặt phẳng cắt
Câu 18: Trình tự đọc bản vẽ chi tiết là:
A. Khung tên, kích thước, hình biểu diễn,yêu cầu kĩ thuật,tổng hợp
B. Hình biểu diễn,khung tên,kích thước, yêu cầu kĩ thuật, tổng hợp
C. Khung tên,hình biểu diễn,kích thước, yêu cầu kĩ thuật, tổng hợp
D. Hình biểu diễn,kích thước,khung tên, yêu cầu kĩ thuật, tổng hợp
Câu 19: Kích thước trên bản vẽ kĩ thuật tính theo đơn vị:
A. mm B. cm C. dm D. m
Câu 20: Bản vẽ lắp có thêm nội dung nào mà bản vẽ chi tiết không có?
A. Hình biểu diễn B. Kích thước C. Bảng kê D. Khung tên
Câu 21: Khi đọc bản vẽ chi tiết phải đọc nội dung gì trước?
A. Hình biểu diễn B. Kích thước C. Yêu cầu kĩ thuật D. Khung tên
Câu 22: Trình tự đọc bản vẽ lắp là:
A. Khung tên,bảng kê, hình biểu diễn, kích thước, phân tích chi tiết, tổng hợp
B. Khung tên, hình biểu diễn,bảng kê, kích thước, phân tích chi tiết, tổng hợp
C. Khung tên, hình biểu diễn, bảng kê, phân tích chi tiết, kích hước, tổng hợp
D. Hình biểu diễn, khung tên, bảng kê, phân tích chi tiết, kích thước, tổng hợp
Thu gọn
Câu 12. D
Câu 13. A
Câu 14. B
Câu 15. B
Câu 16. C
Câu 17. B
Câu 18. C
Câu 19. A
Câu 20. C
Câu 21. D
Câu 22. A
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a.H là trung điểm của AB, M là trung điểm SD, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy
a. tính d(AM,SC)
b. tính d(D,(SHC))
Giúp em với ạ!! em cảm ơn nhìu<3
Tam giác SAB đều \(\Rightarrow SH\perp AB\)
Mà \(\left\{{}\begin{matrix}AB=\left(SAB\right)\cap\left(ABCD\right)\\\left(SAB\right)\perp\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SH\perp\left(ABCD\right)\)
Gọi N là trung điểm SC \(\Rightarrow MN\) là đường trung bình tam giác SCD
\(\Rightarrow\left\{{}\begin{matrix}MN||CD\\MN=\dfrac{1}{2}CD\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}MN||AH\\MN=AH\end{matrix}\right.\) \(\Rightarrow AMNH\) là hbh
\(\Rightarrow AM||HN\Rightarrow AM||\left(SHC\right)\)
\(\Rightarrow d\left(AM;SC\right)=d\left(AM;\left(SHC\right)\right)=d\left(A;\left(SHC\right)\right)\)
Mặt khác H là trung điểm AB \(\Rightarrow d\left(A;\left(SHC\right)\right)=d\left(B;\left(SHC\right)\right)\)
Từ B kẻ \(BE\perp HC\Rightarrow BE\perp\left(SHC\right)\) (do \(SH\perp BE\))
\(\Rightarrow BE=d\left(B;\left(SHC\right)\right)\)
Hệ thức lượng: \(BE=\dfrac{BH.BC}{CH}=\dfrac{BH.BC}{\sqrt{BH^2+BC^2}}=\dfrac{a\sqrt{5}}{5}\)
b.
Từ D kẻ \(DF\perp HC\Rightarrow DF\perp\left(SHC\right)\) (do \(SH\perp DF\))
\(\Rightarrow DF=d\left(D;\left(SHC\right)\right)\)
\(DF=DC.cos\widehat{FDC}=DC.cos\widehat{BCH}=\dfrac{DC.BC}{CH}=\dfrac{DC.BC}{\sqrt{BC^2+BH^2}}=\dfrac{2a\sqrt{5}}{5}\)
Cho hình chóp SABCD có đáy là hình thang vuông tại A;B với BC là đáy nhỏ. Biết rằng tam giác SAB đều có cạnh là 2a và nằm trong mặt phẳng vuông góc với đáy, S C = a 5 và khoảng cách từ D tới mặt phẳng (SHC) là 2 a 2 (H là trung điểm của AB). Thể tích khối chóp S.ABCDlà:
A. a 3 3 3
B. a 3 3
C. 4 a 3 3 3
D. 4 a 3 3
Đáp án là C

ta có S A B ⊥ A B C D S A B ∩ A B C D = A B S H ⊥ A B ⇒ S H ⊥ A B C D
mà D I ⊥ C H D I ⊥ S H ⇒ D I ⊥ S H C ⇒ d D , S H C = D I = 2 a 2
ta có
Δ B H C = Δ A H E ⇒ S Δ B H C = S Δ A H E ; H E = H C
mà
S A B C D = S A H C D + S Δ B H C = S A H C D + S Δ A H E = S Δ D C E
Tam giác SAB đều nên . S H = a 3
Tam giác SHC có
H C = S C 2 − S H 2 = a 2 ⇒ E C = 2 H C = 2 a 2 .
Khi đó S A B C D = S Δ D C E = 1 2 D I . E C = 4 a 2 .
Vậy V A B C D = 1 3 S H . S A B C D = 1 3 a 3 .4 a 2 = 4 a 3 3 3 .